V Если в качестве допустимого упругого поля взять поле, соответствующее автомодельному решению Карозерса (9.7) - (9.8), то простое, но длинное вычисление по указанному рецепту дает нижнюю оценку для C(v):

16 (sin 2а -2acos2a)2 r.j

yf- 4(к + 5)а + 8асоз4а-(х + 7) sin4a *

Здесь x=(3-v)/(H-v).

Эта оценка, представленная на рис. 9.3 (кривая 1) для случая v = 0, обладает очевидными несообразностями. Например, согласно этой оценке, клин теряет жесткость при критических углах, обращающих в нуль числитель формулы (9.37), и задолго до критических углов жесткость начинает убывать с ростом угла а. Последнее заведомо неверно, поскольку для всякого клина поле напряжений клина с любым меньшим углом раствора, продолженное тож-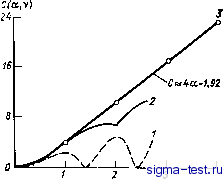

Рис. 9.3. Зависимость безразмерной жесткости клина от его угла раскрытия при v=0.

дественным нулем до границ клина, является допустимым. Таким образом, жесткость является неубывающей функцией угла раствора клина: dC/daO. И действительно, вычисление жесткости на основе неавтомодельного решения при а=а*, данного первыми членами формулы (9.22) и также принадлежащего к допустимым, приводит к ненулевой оценке жесткости. Далее, для углов, не равных критическим, в качестве допустимых брались поля, описываемые суммой решений (9.7) и (9.30), причем коэффициент А в решении (9.30) выбирался так, чтобы минимизировать энергию напряжений W. В качестве к также брался корень уравнения (9.29), дававший минимум энергии напряжений. Соответствующая оценка для жесткости (рис. 9.3, кривая 2) получается значительно более высокой и, что существенно, гладко проходящей через критические углы. Однако эта оценка неудовлетворительна при больших а. В самом деле, при больших а обобщенный клин должен вести себя, как упругое кольцо, для которого во всех точках а0=М/2яг2, arr=OQQ=0, а энергия напряжений равна

(9.38)

следовательно, безразмерная жесткость С (v) составляет C=-M/QG/?2=4rt. Таким образом, при больших а каждое увеличение а на я должно увеличивать безразмерную жесткость на 4я, так что С/а4, и при больших а для С должна быть справедлива асимптотическая формула

C=4a-6(v). (9.39)

Для получения весьма точной оценки безразмерной жесткости Будянский и Кэррьер использовали то обстоятельство, что при а=Ля/2, где - целое число, все корни уравнения (9.29) действительны и выражаются простой формулой

A = mlM-\, (9.40)

где т -целое число. Для упругого поля берется выражение в виде суммы большого числа решений вида (9.30)

(i-,)c.si5s, (+,),) +M?Jzfc

(последний член соответствует корню, равному нулю, и выражается теми же формулами, что и (9.7). Здесь KN, а m - положительное число. Коэффициенты Am выбираются из условия минимальности энергии напряжений W, Результаты соответствующих расчетов представлены на рис. 9.3 кривой 3. Как видно, соответствующая оценка получилась значительно более высокой и, что важно, она согласуется с формулой (9.39). Для 6(v) вычисления дали следующие значения: 6(0) = 1,92; 6(0,25) =1,68; 6(0,5) = 1,48.

Этот пример показывает, что автомодельные решения могут быть с успехом использованы для получения оценок суммарных характеристик неавтомодельных решений невырожденных задач. Проведенное Будянским и Кэррьером исследование показало, однако, что такое использование автомодельных решений следует делать весьма осмотрительно. В самом деле, например, при всех а < решение на больших расстояниях от вершины клина хорошо аппроксимируется решением Карозерса. Казалось бы, отсюда следует возможность использования этого решения при а< <а для оценки жесткости. Это привело, однако, к противоестественному убыванию жесткости, что связано с непригодностью автомодельного решения для описания упругого поля вблизи г = R, вносящего существенный вклад в энергию напряжений.

9.4. Законы подобия хрупкого и квазихрупкого разрушения

1. Классическая линейная теория упругости не позволяет непосредственно определить прочность конструкции: в ней можно построить решение для сколь угодно больших нагрузок. В то же время для многих материалов (металлов, полимеров, керамик) деформации перед разрушением при обычных условиях малы и пластические деформации либо отсутствуют вовсе (хрупкое разрушение), либо сосредоточиваются в малой окрестности разрыва (квазихрупкое разрушение), так что, казалось бы, классическая теория упругости должна быть применимой. По этой причине первоначально предлагавшиеся теории прочности дополняли теорию упругости локальными условиями разрушения. По существу эти условия ограничивали возникающие напряжения характерной для данного материала постоянной. Считалось, что разрушение начи-

нается, когда где-то в теле достигается предельное значение некоторой комбинации компонентов напряжения и притом там, где оно достигается.

Важнейший шаг в построении модели хрупкого разрушения сделал Гриффите [133]. Он понял, Что задавая конструкцию в ее идеальном виде, в котором она предстает на чертеже, мы не полностью определяем границы тела. В действительности помимо законных границ в любом изделии всегда имеются дефекты - трещины, поверхность которых также составляет часть границы. Теории прочности упомянутого выше типа, дополняющие теорию упругости ограничением на напряжения, для расчета прочности тел с трещинами не годятся принципиально: на краю трещины напряжения получаются, согласно теории упругости, бесконечными. Трещины способны расширяться с увеличением нагрузок; это делает задачу теории упругости для тела с трещинами нелинейной. Следовательно, в задаче разрушения должна быть существенной некоторая характеристика сопротивления материала распространению в нем трещин. В качестве такой характеристики Гриффите выбрал энергию образования единицы поверхности трещины. Ирвин [141] и Орован [178] распространили концепцию Гриффитса на квазихрупкое разрушение и тем расширили область ее применения. В работе [9] был предложен силовой подход к теории хрупкого и квазихрупкого разрушения, основанный на явном учете дополнительных к основным нагрузкам сил сцепления, действующих на поверхности трещин, и условии ограниченности напряжений в концах трещин, указанном С. А. Христиановичем [37, 23]. Было показано, что определение прочности математически приводится к глобальной задаче отыскания области существования (по параметрам нагружения) решения нелинейной задачи теории упругого равновесия тел с трещинами. Последняя принадлежит к числу трудных проблем с подвижной границей, так что в сколько-нибудь сложных случаях нельзя рассчитывать на получение аналитического решения. В связи с этим большое значение приобретает эксперимент - физический и численный -а следовательно, выяснение законов подобия. Отсылая за подробностями постановки задачи разрушения к обзорам [142, 10, 88, 24] и монографр-фиям [76, 160, 64, 82], мы остановимся здесь на законах подобия при хрупком и квазихрупком разрушении [10, 11, 131].

Пластическая головка трещины для классического примера квазихрупкого разрушения - трещины в органическом стекле - представлена на рис. 9.4 а [210]. Как видно, размер головки мал, он имеет порядок нескольких сотых миллиметра. За поверхность трещины при таком квазихрупком разрушении принимается граница упругой и пластической областей. При этом подходе в дополнение к основным нагрузкам нужно учесть силы G{s) (рис. 9.4 б), действующие со стороны пластической головки на упругую область. В случае чисто хрупкого разрушения такие силы тоже существуют; это молекулярные силы сцепления. Поэтому силы G{s) объединяются под общим названием сил сцепления.