с показателем степени, зависящим от глобального числа Рейнольдса. Здесь обозначено x(Re) = 1/Ф(Ке). Степенные законы распределения скорости в различных турбулентных сдвиговых течениях уже давно предлагались в качестве эмпирических зависимостей. Они прекрасно подтверждаются многочисленными экспериментами, среди которых следует отметить классические опыты с турбулентными течениями в гладких трубах Мёбиуса [190], Ни-курадзе [172] и сравнительно недавние превосходные измерения

JO

Рис. 11.2. Универсальный логарифмический закон на первый взгляд подтверждается данными измерений распределений скорости в гладких трубах, пограничных слоях, на гладких пластинах и т. д.

1) Re=4,I . 103; 2) Re=2,3 10; 3) Re=l,l 10; 4) Re=4,0 lO; 5) Re = l.l Ю; 6) Re = =2,0 10; 7) Re=3,2.10s (опыты Никурадзе); 8) опыты Райхардта.

Лауфера [158]. Признано (см. монографии Шлихтинга [191] и Хинце [138]), что степенные законы для распределения скорости с показателем степени, зависящим от глобального числа Рейнольдса, подтверждаются заведомо не хуже, чем универсальный логарифмический закон. На рис. 11.3 представлено заимствованное из монографии Шлихтинга [191] распределение скоростей в гладких трубах, построенное по измерениям Никурадзе [172], которое удовлетворительно подтверждает степенное распределение скоростей почти по всему сечению трубы. Тем не менее считается, что универсальный логарифмический закон имеет, в отличие от степенных, теоретическое обоснование, а степенные законы представляют собой просто эмпирические соотношения. На самом деле,

как мы видели, степенные законы обосновываются исходя из предположения о неполной автомодельности потока по локальному числу Рейнольдса не хуже, чем универсальный логарифмический закон обосновывается исходя из предположения о полной автомодельности.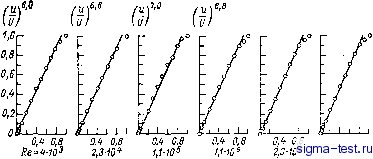

ом 0,8 zIR

Рис. 11.3. Измерения Никурадзе подтверждают степенной закон распределения скорости почти по всему сечению трубы.

и - средняя скорость на оси трубы.

Данные опытов названных выше авторов позволяют определить зависимость A.(Re) (рис. 11.4, кривая /) до Re 10. Остается неясным поведение этой зависимости при еще больших значениях Re: стремится % при возрастании Re к нулю или к некоторому

Рис. 11.4. Зависимости X(Re*) (7) и >c(ReJ (2), определенные по данным измерений распределения скорости в гладких трубах, и зависимость глобального числа Рейнольдса Re от обычного числа Рейнольдса Re, основанного на средней скорости (3).

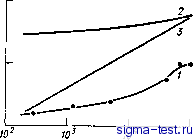/Re-

постоянному пределу, отличному от нуля? Последнее означало бы, что универсальный логарифмический закон, строго говоря, вообще не имеет места даже при очень больших числах Рейнольдса и является лишь приближенным представлением опытных данных. Упомянутые опыты позволяют также построить зависимость x(Re) (см. рис. 11.4, кривая 2). Как видно, величина x(Re) при возрастании Re , меняется сравнительно слабо и в первом приближении ее можно считать постоянной.

11.2. Пристеночная область турбулентного потока

с поперечным сдвигом - полуэмпирическая теория и гипотезы

автомодельности Колмогорова

Рассмотрим теперь пристеночную область турбулентного потока с поперечным сдвигом, описанную в п. 11.1, более детально, опираясь на полуэмпирическую теорию, предложенную А. Н. Колмогоровым [55]. Теория Колмогорова основана на использовании уравнений сохранения импульса и турбулентной энергии и их замыкании при помощи некоторых гипотез автомодельности.

Исключим из рассмотрения весьма тонкую область в непосредственной близости от стенки, где вязкие напряжения сравнимы с турбулентными. Тогда уравнение баланса импульса для пристеночной области потока с поперечным сдвигом записывается в виде

-р<иш> = т. (11.8)

Здесь и - пульсации соответственно продольной и вертикальной компонент скорости; р - плотность жидкости; -р <аг(у>- средний поток продольной компоненты импульса через единичную горизонтальную площадку, т. е. напряжение сдвига, создаваемое турбулентностью; т - действующее напряжение трения, по условию постоянное. В уравнении (11.8) мы пренебрегли вкладом вязких напряжений по сравнению со вкладом турбулентных напряжений Рейнольдса. Уравнение баланса турбулентной энергии для потока с поперечным сдвигом записывается в том же пренебрежении вкладом вязких напряжений в виде [69]

(uWy д,и + <[р7р + (1/2) {и + V + w> + 8, = 0. (11.9)

где и - пульсация поперечной компоненты скорости, - пульсация давления, - средняя скорость диссипации турбулентной энергии в единице массы жидкости. Уравнение (11.9) получается по общему правилу, изложенному в п. 10.1, и отражает тот простой факт, что локальный баланс турбулентной энергии складывается из притока турбулентной энергии от энергии среднего движения, т. е. за счет работы рейнольдсовых напряжений (первый член), диффузионного притока турбулентной энергии (второй член) и диссипации турбулентной энергии в тепло. Для интересующих нас задач перенос турбулентной энергии за счет диффузии мал, и им можно пренебречь.

Введем коэффициент обмена импульса К посредством соотношения

/ит} = -Кд,и, (11.10)

Подчеркнем, что для потока с поперечным сдвигом соотношение (11.10) представляет собой простое переобозначение и не несет в себе никакой дополнительной гипотезы.

Как уже говорилось, турбулентный поток представляет собой совокупность множества вихрей, пронизывающих поток и создающих нерегулярное, быстро меняющееся движение. Гипотеза