что решение быстро выходит на автомодельную асимптотику следующего вида:

P = Po(rД)(r/rf, у, vi); P = 9oR{rlrf, у, vi);

V = (гIt) V {rlrf. y. yO; Tf = (AtV\ (4.10)

где A и a - некоторые постоянные. При этом оказалось, что постоянная а зависит только от y и Yi и не зависит от начальных ус-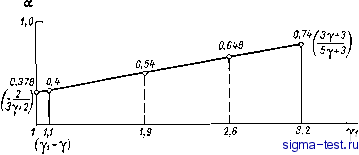

Рис. 4.3. Зависимость собственного значения а от эффективного показателя адиабаты на фронте волны yi при у=1Л.

при Yi<V а<2/5; при Vi>V а>2/5; при Yi=V (адиабатический сильный взрыв) а=2/5; при Yi=2y+1 а= (3y+3)/(5y+3) (детонация с переменной скоростью распространения детонационной волны; удовлетворяется условие Чепмена-Жуге).

ловий (брались разные /о, Е, ро). Зависимость a(Yi) при y=1.I приведена на рис. 4.3. Постоянная А получилась зависящей также и от начальных условий (начальный момент /о, начальная энергия £, начальная плотность ро). Выход на автомодельный режим показан на графике зависимости 1п г/ от 1п которая быстро выходит на прямую 1пг/а1п/, и на графике зависимости

Таблица 4.1

1п d&/dt от 1п которая так же быстро выходит на прямую In d/dt {5а -3)lnt (дляY=l,9; Yi = 1Д см. рис. 4.1), а также на графиках зависимости величины p/pf от г/г/ для разных моментов времени (рис. 4.2).

4.4. Автомодельное предельное решение

Выясним теперь, каким образом в численном эксперименте появилась автомодельная промежуточная асимптотика (4.10).

По сравнению со случаем точечного взрыва (начальные условия (2.19)) в задаче, решавшейся в численном эксперименте, к определяющим параметрам задачи добавляется еще /?о, так что появляется не одна, а две безразмерные независимые переменные:

l = r(Et%o)-; ц = Но(Е1роУ\ (4.11)

И скорость, плотность и давление газа, согласно анализу размерностей, выражаются в виде

v = {r/t)V {1, 11, Y, Yi); 9 = 9oR{b Y, Yi);

P = 9o{rVt)P{b ri. Y, Yi). (4.12)

Решение задачи о сильном точечном взрыве при Y = Yi представляет собой, с одной стороны, решение сингулярной предельной задачи, соответствующей /?о = 0, с другой стороны,- асимптотику решения (4.12) при t-oo. Как мы выяснили, при YitY решения предельной задачи, соответствующей Ro = О, не существует. Нас, однако, интересует не решение предельной задачи, а асимптотическое представление решения неавтомодельной задачи с ЯоФО при больших t. При возрастании же и фиксированном г к нулю стремятся как g, так и т]. Появление у решения автомодельной промежуточной асимптотики (4.10) объясняется тем, что существует такое положительное число р, зависящее от Y и Yb что при g, т] О главные члены асимптотических представлений функций Р, У, R имеют вид

Р = Р il/rf); У==У{1/ц); R = R il/rf), (4.13)

Именно поэтому предельное движение автомодельно, так как

где В = (£/ро)(-Р)/ а = 2(1-р)/5.

Класс автомодельных решений уравнений газодинамики, к которому принадлежит предельное решение исследуемой задачи (4.13), был указан К. Бехертом [ПО] и Г. Гудерлеем [134] и в дальнейшем рассматривался Л. И. Седовым [95] и другими авторами.

Для дальнейшего анализа удобно перенормировать автомодельную независимую переменную и взять ее в виде

с = const = г (Ж/ро)- - А = oERl - Р\ (4.14)

где постоянный параметр а выбран так, чтобы на фронте ударной волны значение автомодельной независимой переменной было равно единице (?= 1). При этом асимптотический закон распро-

странения ударной волны записывается в виде, согласующемся с (4.10):

г=(Л/ро)<-Р¥<-Р (4.15)

Заметим теперь, что стремление g и т] к нулю можно осуществлять иначе: потребовать, чтобы при фиксированных rut величина Е стремилась к бесконечности (или нулю), а Ro - k нулю. Однако чтобы получилась та же асимптотика, что и для рассматриваемого неавтомодельного решения при больших временах, произведение должно при этом оставаться постоянным:

£/?Р/(-Р) = const. (4.16)

Таким образом, при у\фу автомодельное предельное движение соответствует не точечному взрыву, т. е. не выделению в начальный момент в центре взрыва конечной порции энергии, а выделению в конечной области радиусом Rq порции энергии £, стремящейся при /?о-0 к нулю или бесконечности, в зависимости от знака р.

Параметр р, или, что то же, а, при данных y и yi можно определить двумя способами. Во-первых, можно проследить, (например, численно) эволюцию неавтомодельного решения исходной задачи до ее выхода на автомодельную асимптотику: этот способ был продемонстрирован в предыдущем разделе. Во-вторых, можно воспользоваться тем, что автомодельная асимптотика сама является решением уравнений газодинамики, удовлетворяющим определенным условиям, и попытаться построить это решение и попутно определить показатель а.

Рассмотрим теперь второй способ. Итак, искомое предельное решение ищется в виде

P = 9rlt)P {1 Y. Yi); P = Po/?(S, Y. Yi);

v = mV{ly>yi)\ = rlrf; (4.17)

Подставим это решение в уравнения газодинамики (4.5). Получаем, следуя обычной технике [134, 97], одно уравнение первого порядка

[2(1/-1)+3(у-1)1/][(К-а)2-г]

dV V -о.

[(31/-X) 2-1/(К-1) (1/-а)]

+ Y- Ij

(4.18)

>c = 2(l-a)/Y; z = yPIR, и два других уравнения первого порядка d\ni z-{V -а)2

dV l/(l/-l) {V -a) + (K-3V)z

(4.19)

d\nl 2- (K -a)2 -