

 |
 |
|
|
Навигация
Популярное
|
Публикации «Сигма-Тест» Промежуточная асимптотика (развивающееся направление) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 [ 26 ] 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 Движение, возникающее в каждом из полупространств л:0, отвечает обычному симметричному плоскому сильному взрыву с энергиями 2Ei и 2Е2 и начальными плотностями pi и ро. Однако при симметричном взрыве давление р(0, t) в плоскости х = 0 составляет определенную часть давления на фронте, зависящую только от Y- Это элементарно вытекает из анализа размерностей. Отсюда и из непрерывности давления при х = 0 следует, что p/i = = Р/2. Из этого равенства и соотношений (4.56) -(4.57) находим Ci = -Vpo/Pi. (4.58) Простой подсчет показывает также, что £2/£i = VPi/Po- Таким образом, для сосредоточенного взрыва в пределе при pi/po-0 получается, что вся энергия мгновенно уходит в пустоту. Ясно, однако, что асимптотика, отвечающая сосредоточенному взрыву на границе полупространств, устанавливается не сразу. Действительно, как и в п. 4.6, мы приняли, что в момент t = x вся энергия сосредоточена в некотором слое более плотного газа, имеющем конечную толщину. С началом движения начинается перераспределение энергии между полупространствами. Естественно думать, что при малых pi/po в начальный период, когда скорость распространения левой волны, идущей по менее плотному газу, много больше характерной скорости VPo/Po, движение вблизи правой волны будет близко к движению газа при коротком ударе, рассмотренному в предыдущих параграфах. Выше было показано, что это движение выходит на автомодельную асимптотику за время порядка т. Это хорошо подтверждает численный расчет неавтомодельной задачи с начальными условиями: v = 0 v = 0 v = 0 p = Di = 0,l; p = 0 при JC < 0; P = Po=l; P=I приО<л:<1; P = Po=l; P = 0 npHJC>l; (4.59) Результаты расчета представлены на рис. 4.7, на котором приводится относительное распределение давления р/р/2 в функции t = x/xf2 для разных моментов времени t. Кривые I и II соответствуют автомодельным распределениям для короткого удара и сосредоточенного сильного взрыва. Как видно, существует определенный интервал времен ti<t<it2 (для рассчитанного примера 1 = 2,5; 2 = 40), настолько больших, чтобы движение с достаточной точностью стало автомодельным и, вместе с тем, настолько малых, чтобы влияние конечности плотности газа слева было пре-небрежимым. В этом интервале времен в области существенного изменения давления вблизи правой волны действует автомодельная промежуточная асимптотика короткого удара. При t > /3 (в рассмотренном примере /3= 100) область существенного изменения давления описывается автомодельной промежуточной асим- птотикой сильного взрыва, пока не начинает сказываться (ср. главу 2) начальное давление невозмущенного газа. Анализ промежуточных асимптотик в задаче о взрыве вблизи границы раздела, изложенный выше, и численные эксперименты Рис. 4.7. Решение задачи о взрыве на границе раздела выходит на промежуточные асимптотики сначала короткого удара (I), потом сильного взрыва ( ). Крестики соответствуют =100. 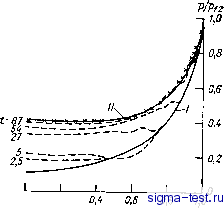 X/Xf2 0,2 были Проведены И. О. Власовым, А. И. Державиной и О. С. Рыжовым [31]. В. П. Пархоменко, С. П. Поповым и О. С. Рыжовым [83, 84] был проведен соответствующий анализ и для задач с осевой и сферической симметрией. Вместо решения типа короткого удара, которого для таких симметрии не существует, в этих задачах появляются другие промежуточные асимптотики-автомодельные решения второго рода, отвечающие течениям со стоками переменной интенсивности на оси или в центре симметрии. Глава 5 КЛАССИФИКАЦИЯ АВТОМОДЕЛЬНЫХ ЗАВИСИМОСТЕЙ И АВТОМОДЕЛЬНЫХ РЕШЕНИЙ 5.1. Полная и неполная автомодельность В главах 2-4 было рассмотрено несколько показательных и принципиально различных автомодельных задач. В задачах о распространении сильных тепловых и сильных взрывных волн и в задаче о мгновенном точечном тепловом источнике ситуация оказалась относительно простой. Для этих задач существует некоторая предельно схематизированная вырожденная постановка (выделение энергии в точке, равенство нулю начальных температуры и давления). Оказалось, что, рассматривая эту постановку задачи и стандартным образом применяя к ней процедуру анализа размерностей, можно обнаружить автомодельность решения, выяснить строение автомодельных переменных и благодаря наличию некоторого интеграла получить решение в конечном виде: Более глубокое рассмотрение показывает, однако, что эта простота иллюзорна, и, например, делая предположение о точечном выделении энергии, мы, что называется, ходили по краю пропасти. Действительно, слегка, на первый взгляд, изменив постановки задач и притом так, что, казалось бы, все те же соображения подобия должны сохранить силу, мы пришли к противоречию. Как оказалось, в модифицированных задачах нужных нам решений просто не сугцествует. Более детальный анализ показал, что при попытке поиска решений модифицированных задач тем же стандартным способом исходя из формулировки вырожденной задачи оказалась неправильной сама постановка вопроса. На самом деле нам были нужны не точные решения упрощенно сформулированных вырожденных задач, соответствующих мгновенному отбору в точке конечной массы жидкости или мгновенному выделению в точке конечной порции энергии. Нас интересуют асимптотики решений невырожденных задач при больших временах. Мы применили анализ размерности к невырожденным задачам, существование и единственность решений которых либо строго доказаны, либо не вызывали сомнений; невырожденные задачи, естественно, перестали быть автомодельными. Предельный переход при стремлении к нулю дополнительного параметра, делавшего задачи неавтомодельными, оказался в модифицированных задачах нерегулярным: в одном случае предел получился равным нулю или бесконечности в зависимости от условий задачи, в другом случае выяснилось, что его просто не существует. Тем не менее оказалось, что в обоих случаях осмысленные промежуточные асимптотики существуют и, более того, они автомодельны. Выяснилось, что именно эти асимптотики и есть то, что нам на самом деле нужно. Оказывается, отбор массы при фильтрации в упругопластической пористой среде и выделение энергии при сильном взрыве с притоком или потерями энергии на фронте нельзя считать точечными. Уменьшая размер области, где происходит первоначальное выделение энергии или отбор массы жидкости, необходимо для получения правильной асимптотики решения исходной невырожденной задачи при больших временах соответствующим образом увеличивать или уменьшать отбираемую массу или выделяемую энергию так, чтобы был постоянным некоторый момент начального распределения массы или энергии. Существенно, что степень, в которой длина входит в выражение этого момента, заранее не задана, и ее принципиально нельзя определить из соображений размерности, а нужно найти в ходе решения задачи определения автомодельной асимптотики. Таким образом, мы столкнулись с существованием автомодельных решений двух типов.
|
|
© 2010 www.sigma-test.ru Санкт-Петербург: +7 (812) 265-34-48, +7 (812) 567-94-10
Разработка и поддержка сайта: +7(495)795-01-39 после гудка 148651, sigma-test.ru(my_love_dog)r01-service.ru Копирование текстовой и графической информации разрешено при наличии ссылки. |