(силы, отнесенной к длине) 5 и силы 5. Значения этих параметров, отвечающие разрушению, о/, 5/, S/ при хрупком или квазихрупком разрушении тела заданной формы определяются двумя размерными параметрами - модулем сцепления К и размером тела /. Размерные упругие постоянные не входят в число определяющих параметров, так как при задании действующих на тело нагрузок поле напряжений от них не зависит.

Как видно из анализа размерностей, при квазихрупком и хрупком разрушении определяющих параметров подобия нет, следовательно,

S/ = const/(/ = constО; = const icr\ (9.48)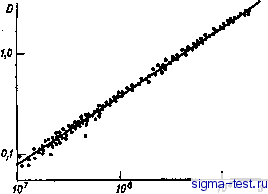

Рис. 9.6. Обработка опытных данных по распространению конической трещины подтверждает [111] полную автомодельность процесса.

Постоянные в (9.48) можно поэтому определить из опыта на геометрически подобной модели из любого материала, также разрушающегося по квазихрупкому механизму, так что, например,

= {K)K)nfy\ (9.49)

Здесь индексы р относятся к натуре, m - к модели. Единственным требованием к модельной конструкции является ее геометрическое подобие натурной конструкции, в том числе подобие начальных трещин.

Если пластические деформации в материале при разрушении не сосредоточены вблизи трещины, а занимают заметную часть конструкции (в этом случае разрушение несколько неудачно называется вязким), то появляется новый размерный определяющий параметр: предел текучести Оу Следовательно, появляется определяющий параметр подобия

1 = Оу/Г1К, (9.50)

который мы будем называть параметром Ирвина: в его работе [143] (см. также обзор и обсуждение в [131]) было впервые установлено определяющее влияние параметра, эквивалентного /, на вязкое разрушение и переход от квазихрупкого разрушения к вязкому.

Таким образом, для параметров вязкого разрушения получаем Sf = avPOs{I)\ Sf = OylOs{I); Gf = oyOa{I). (9.51)

Параметр / представляет собой корень квадратный из отношения масштаба конструкции / к характерному масштабу материала KGY-характерному размеру пластической зоны вблизи края

трещины. Поэтому испытания на модели из того же материала при тех же внешних условиях проводить нельзя. В работе В. М. Вайншельбаума и Р. В. Гольдштейна [131] предложено проводить моделирование путем испытаний модели из того же материала при других температурах: масштаб /CVo сильно зависит

от температуры, увеличиваясь с ее возрастанием.

Глава 10

ПОЛНАЯ И НЕПОЛНАЯ АВТОМОДЕЛЬНОСТЬ В ТЕОРИИ ТУРБУЛЕНТНОСТИ. ИЗОТРОПНАЯ ОДНОРОДНАЯ ТУРБУЛЕНТНОСТЬ

10.1. Проблема турбулентности

Эта и следующая главы отличаются тем, что здесь автомодельность (полная и неполная) будет устанавливаться с существенным использованием экспериментальных данных и без обращения к математической формулировке задачи, которая в настоящее время для турбулентности отсутствует.

Проблема турбулентности, которой посвящены эти главы, с полным основанием считается проблемой номер один современной классической физики. Само явление турбулентности, как известно, состоит в следующем. Как мы убедились в главе 1, основным параметром подобия, определяющим глобальные свойства течения несжимаемой вязкой жидкости, является число Рейнольдса Re = p[ /x (р - плотность, \х - вязкасть жидкости, U - характерная скорость, / - характерный размер потока). Когда число Рейнольдса переходит через определенное критическое значение Rccr, разное для разных потоков (например, для течения в гладкой цилиндрической трубе круглого поперечного сечения Recr= 10 для течения в пограничном слоеНссг. Ю), характер течения внезапно и резко меняется. Поток из регулярного, упорядоченного, ламинарного, каким он был при докритических значениях числа Рейнольдса, становится существенно нерегулярным. Течение при сверхкритических значениях числа Рейнольдса резко и неупорядоченно меняется в пространстве и во времени, и поля характеристик потока (давления, скорости и т. д.) можно с хорошим

приближением считать стохастическими, случайными. Такой режим течения называется турбулентным,

В настоящее время по поводу возникновения турбулентности существуют лишь более или менее правдоподобные гипотезы, порой весьма интересные, но не имеющие доказательной силы. Не существует также законченного математического описания сформировавшихся турбулентных потоков. В этих обстоятельствах при всех попытках создания теоретических моделей тех или иных классов турбулентных течений соображения подобия занимают первостепенное место.

Вместе с большинством исследователей мы будем исходить из того, что при малых по сравнению со скоростью звука скоростях истинное турбулентное движение описывается уравнениями движения вязкой несжимаемой жидкости, т. е. уравнениями сохранения импульса Навье-Стокса и уравнением неразрывности, которые в прямоугольных декартовых координатах Хг записываются в виде

diUi + UdaUi - diplp + vAUu а а = 0. (10.1)

Здесь - компоненты вектора скорости, v = р/р - кинематическая вязкость, р - давление; по повторяющимся греческим индексам предполагается суммирование от единицы до трех,

Строить решение этих уравнений, отвечающее некоторой конкретной реализации развитого турбулентного течения, невозможно ввиду его крайней неустойчивости. Поэтому, а также ввиду отмеченной выше возможности считать характеристики поля турбулентного потока случайными, описание турбулентных течений всегда ведется в статистических терминах. Как известно (подробнее см. в монографии А. С. Монина, А. М. Яглома [74, 75]), достаточно полное описание развитого турбулентного потока дается системой средних величин

<t/,(x, t)\ <р(х, t)y (10.2)

и моментов, т. е. тензоров вида

Bifk . = <tii{x, t)Uj{xu t)Uk{x2y t) ...>; Pt7... = <p(x, t)Ut{xu t)Uj{x2, t) ...>; .................. (10.3)

для всевозможных точек и систем точек х; х, xf, х, хь хг; ... .

Здесь знак <.. .> обозначает вероятностное среднее значение Вероятностное среднее значение используется в теоретических ра ботах по турбулентности в качестве естественного способа осред нения. На опыте осреднение производится по объему или по вре мени; отождествление этих типов осреднения между собой и с ве роятностным осреднением делается на основе так называемой эр годической гипотезы.

Система уравнений для моментов получается умножением уравнений (10.1) на компоненты скорости в различных точках по-