дящейся на единицу толщины.) В силу соотношений (9.2), размерность функции напряжений также совпадает с размерностьк> силы, поэтому анализ размерностей после стандартной процедуры приводит к соотношению

=Л1Ф(0, а). (9.4)

Подставляя (9.4) в (9.3), получаем для Ф (6, а) обыкновенное дифференциальное уравнение

ф + 4ф = 0. (9.5)

Боковые стороны клина свободны от напряжений на всем своем протяжении:

а00(г, dza) = 0; а,е(г, ±а) = 0,

откуда и из выражений (9.2), (9.4) получаются граничные условия для функции Ф(0, а):

еФ(+а, а) = 0. (9.6)

Уравнение и граничное условие определяют решение с точностью до множителя, который находится из следующего условия. Проводится разрез по окружности произвольного радиуса, вычисляется суммарный момент сил, действующих на отрезанную часть клина со стороны разреза, и результат приравнивается моменту приложенной в вершине пары М - отрезанная часть клина должна быть в равновесии. В результате окончательные выражения получаются в виде:

для функции напряжений

цг==м{20 cos 2а - sin 2е)/2 (sin 2а - 2 а cos 2а), (9.7)

для компонент поля напряжений

2М sin 29 М (cos 2а -cos 29)

(sin 2а-2а cos 2а) г2 ~ (sin 2а - 2а cos 2а) г2 (00 -

(9.8)

9.2. Парадокс Стернберга-Койтера. Промежуточная асимптотика решения неавтомодельной задачи

В замечательной работе Стернберга и Койтера [194] было впервые обращено внимание на странное свойство полученного решения (9.7) -(9.8). При приближении угла а к значению а = = а0,715я, вполне допустимому по физике задачи, при котором обращается в нуль знаменатель выражений {9.7) - (9.8), напряжения во всех точках клина, согласно (9.8), стремятся к бесконечности. В связи с этим возник следующий вопрос: является ли сингулярное автомодельное решение вырожденной задачи (9.7) асимптотикой каких-то неавтомодельных решений невырожденных задач, иными словами, имеет ли оно смысл? Для того чтобы это

выяснить, Стернберг и Койтер рассмотрели для того же бесконечного клина следующую невырожденную задачу (рис. 9.2 а). На конечных отрезках боковых сторон клина 9 = ±а, О г го; по некоторому закону распределены антисимметричные нормальные напряжения, статически эквивалентные паре с моментом М. Касательные напряжения всюду на боковых сторонах клина по-прежнему равны нулю. Таким образом, для невырожденной задачи имеют место условия

Оее(Л а) = -000 (г, -а) = р(г), (Угв{г, а) = Оге{г, -а) = 0 при О < г < оо, (9.9)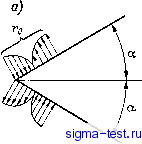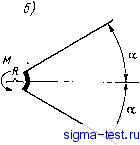

Рис. 9.2. Невырожденные задачи упругого равновесия клина под действием пары сил с моментом М.

а - силы распределены на боковых сторонах клина, б - силы приложены к жесткой подкрепляющей дуге конечного радиуса.

где р(г)-непрерывная функция, тождественно равная нулю при г Го и удовлетворяющая условиям

\p(r)dr = 0; \p{r)rdr= М/2.

(9.10)

Далее, для выделения единственного решения накладывается дополнительное требование регулярности - ограниченности результирующей силы на любом радиальном разрезе клина:

сх5 оо

jo9e(r, e)dr < оо; \агв{г, Q)dr

<оо.

(9.11)

Решение поставленной задачи выполняется применением интегрального преобразования Меллина по переменной г.

Как известно (см., например, [193]), преобразование Меллина функции f(r) и его обращение задаются соотношениями

с + i оо

(9.12)

Применяя преобразование Меллина к бигармоническому уравнению (9.3), получаем для преобразования функции напряжений 4(s, 6) обыкновенное дифференциальное уравнение

[2/92 + 52] [2/92+ (s-f 2)2] (5, 9)=0. (9.13)

Искомое поле напряжений антисимметрично; такой же должна быть и функция напряжений. Общее антисимметричное решение уравнения (9.13) имеет вид

¥(5, 9) = Л (5) sin sB + B (s) sin (5 + 2) 9. (9.14)

Условия (9.9) с учетом (9.2) можно записать в виде

г2д2д(г, ±а)=±р{г)г\ dldWir, ±а)/г] = 0. (9.15)

Преобразуя эти условия по Меллину и интегрируя по частям (для этого нам и нужно было умножать на г), получаем граничные условия для функции 4(5, 9):

¥(5, ± а) = ± р (s)/s (s+1); d¥{s, ±a)/dQO, (9.16)

P{s)=p{r)r + dr. (9.17)

Из (9.14) и (9.16) определяем постоянные A(s) и B(s)\ подставляя результат в формулу обращения, получаем решение для функции напряжений в виде

¥ (г, 9) =

C + i оо

1 f р (s) [s cossa sin (5 + 2) 9 - (s + 2) os (s + 2) a sin s9] r ds

~ cJioo s(5 +1)[(5+1) sin 2a-sin 2(s+l)a]

(9.18)

Выражения для компонент тензора напряжений получаются отсюда дифференцированием:

C + ioo

1 Г p(s)\s cos sa sin (5 + 2) 9 - (s + 2) cos (s + 2)a sin 59] Г 2 ds c-i 00 (s+1) sin 2a-sin 2 (s + 1) a

2m У

orr (r, 9) = {P (s) [(s + 2) cos (s + 2) a sin 59 -- (s + 4) sin (5 + 2) 9 cos 5a] r--} ds (5+1) sin 2a- sin 2 (5 + 1) a

Ore (Q) = {P (s) [(5 + 2) cos 5a cos (5 + 2) 9 - 1 Г - (5 + 2) cos (5 + 2) g cos sQ] r] ds 2ш J. (5+1) sin 2a - sin 2 (5 + 1) a

с - i 00

c+i 00

(9.19)

Как видно, подынтегральные функции в интегралах (9.19) - мероморфные функции комплексной переменной 5, полюса которых совпадают с нулями целой функции

(5 + 1) sin 2а - sin 2 (5 + 1) a=G (5, а) (9.20)