процесса расширения в вакуум) выходит на степенную асимптоту, так что

If {U,) = lo (y) nf.

(4.34)

где go(y)-некоторая функция у, а показатель а также зависит от y- Далее, величина плотности на фронте быстро приближается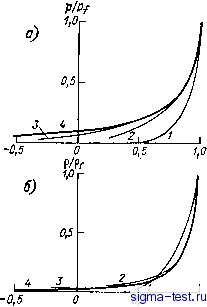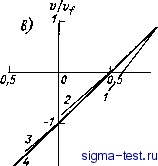

Рис. 4.6. Зависимости р/р/ (а), р/р/ (6), v/vf (в) от x/Xf, полученные численным счетом неавтомодельной задачи о коротком ударе при у=1А [38]. /) /=1,6; 2) /= 5,0; 3) /= 15,6; 4) автомодельная промежуточная асимптотика.

к постоянному значению, а давление и скорость газа на фронте быстро начинают меняться по степенным законам:

Pf/Po ПГ

-2(1-а).

VVpo/Po

(4.35)

Наконец, оказалось, что если построить распределение плотности, давления и скорости в относительных координатах, взяв за масштаб длины х/, а за масштабы характеристик движения Р/, Vf и р/, то эти распределения столь же быстро перестают зависеть от времени (рис. 4.6). Иными словами, оказывается, что решение задачи быстро выходит на автомодельную асимптотику:

lf = lo{y)Uf; Фр=Ф1р(П2ПГ);

ф, = ПГ- Ф1р(П2ПГ); Ф. = ПГ Ф1.(П2ПГ), (4.36)

Выход решения на автомодельную асимптотику происходит не равномерно по области движения - оо < л: а:/(/), а лишь вблизи фронта ударной волны Xf{t) в области тем большей, чем больше прошло времени с начала расширения. Численный счет [38] показал, что на автомодельную асимптотику вида (4.36) с одним и тем же показателем степени а решение выходило независимо от того, было ли давление на стенке в промежуток времени О < < < т постоянным или менялось по различным законам.

4.8. Автомодельное предельное решение

Естественно попытаться построить автомодельное предельное решение непосредственно. Снова ищем его в классе решений Бе-херта-Гудерлея:

P = PoW)P(a, Y); Р = Ро/?(£, Y); v = {xlt)V у);

I = x/Xf = x/At; Xf = ЛР. (4.37)

Здесь Л, а - постоянные. Для функций Р, V, R получается система обыкновенных дифференциальных уравнений, распадающаяся на одно обыкновенное уравнение первого порядка

-([2(y-l) + (Y-I)K](l-a)2-

(Y I) I/ (I/ 1) (F а) - [2 (F - 1) + X (Y - 1)]г}, (4.38)

A={V-a)[y{V-l){V-a) + {K-V)z];

x = 2(I-a)/Y; z = yP/R, (4.39)

и два уравнения первого порядка

d\nl г{У -(х)2

dV ~ V (V-l)(V-a) + (yi-V)z

dinR i/(K-l) (К-а) + (х-К)>г V

dlnl (К~а)[г-(К-а)2] V-a

Таким образом, если известно искомое решение уравнения (4.38), то решения уравнений (4.40) и (4.41) приводятся к квадратурам.

Искомое решение уравнения (4.38) должно проходить через две точки: образ фронта

F=2a/(Y+1); 2: = 2a2Y(Y-l)/(Y+l) (4.42)

й образ свободной границы (особую точку типа седла)

У = у] 2 = 00, (4.43)

причем переменная I при перемещении от особой точки (4.43) к образу фронта (4.42) должна монотонно возрастать. Таким образом, математическая задача оказывается в этом случае близкой

(4.40) (4.41)

к модифицированной задаче о сильном взрыве, рассмотренной в начале этой главы. Мы снова пришли к необходимости провести интегральную кривую уравнения первого порядка того же типа через две точки, одна из которых - особая точка типа седла. Вообще говоря, это невозможно, но, как и в предыдущей задаче, можно показать, что для каждого значения у существует значение а - собственное значение задачи, для которого интегральная кривая уравнения (4.38), проходящая через образ фронта, входит в седло - образ свободной границы. Для различных y во всем диапазоне 1 y оо были получены следующие значения а:

у 1,0 1,1 7/5 Чг 2,8 оо а V2 0,569 0,611 0,627 0,642

Как видно, для всех y в интервале 1 < y < оо справедливо неравенство

У2<а<%

Как и в предыдущих задачах, здесь оказалось, что значения показателя степени а, определенные при непосредственном построении автомодельного предельного решения задачи о коротком ударе, хорошо согласуются со значениями, полученными численным счетом асимптотики решения неавтомодёльной задачи.

Автомодельное предельное решение (4.37) непосредственным построением определилось с точностью до постоянной Л; из (4.37) и (4.34) видно, что

= go(y)VpT- . (4.44)

Таким образом, если мы хотим получать одну и ту же асимптотику, уменьшая время т воздействия импульса на газ, мы должны соответственно увеличивать давление по закону

Ро = const т \ (4.45)

4.9. Законы сохранения энергии и импульса в задаче о коротком ударе

Количество газа, вовлеченного в каждый момент в движение, приходящееся на единицу площади границы, конечно. Поэтому в задаче имеют место законы сохранения импульса и энергии, справедливые и на неавтомодельной стадии движения. Естественно, приходит мысль воспользоваться этими законами для определения показателя степени а и постоянной А автомодельного предельного решения, подобно тому, как это было сделано в главе 2 для рассмотренных там автомодельных решений первого рода.

Напомним, что решение задачи о коротком ударе было получено значи- тельно раньше решения модифицированной задачи о сильном взрыве.