Как видно, если построено нужное решение уравнения (4.18), решение уравнений (4.19) и (4.20) сводится к квадратурам.

Существенно, что искомое решение уравнения первого порядка (4.18) должно проходить через две точки: точку -образ фронта ударной волны и точку -образ центра симметрии. Подставляя (4.17) в условия на фронте (4.9), находим:

откуда следует, что образом фронта в плоскости г, V будет точка

V = 2a/(Yi +1); г = 2aY (yi - 1)/(Yi + (4.22)

Образом центра симметрии ( = 0) в плоскости г, V будет особая точка типа седла уравнения (4.18)

y = 2(l-a)/3Y; =оо. (4.23)

Здесь использовано условие отсутствия притока вещества и энергии в центре взрыва при t > 0. При этом автомодельная переменная ? в ходе перемещения от образа центра симметрии к образу фронта должна монотонно возрастать от нуля до единицы. Вообще говоря, при произвольном а удовлетворить этим условиям невозможно: нельзя провести интегральную кривую уравнения первого порядка через две произвольные точки. Мы увидим, однако, что существуют такие исключительные значения а, для которых это возможно. Таким образом, мы снова пришли к нелинейной задаче на собственные значения: построить интегральную кривую уравнения первого порядка (4.18), проходящую через две точки (4.22) и (4.23), и определить значение параметра а, при котором такое решение существует, т. е. собственное значение задачи.

4.5. Качественное исследование нелинейной задачи на собственные значения

Рассмотрим фазовый портрет -картину интегральных кривых в первом квадранте - интересующей нас части плоскости zV. В случае y < 2, 1 Yi < 2y+1 фазовый портрет представлен на рис. 4.4, где кривые 1-3 соответствуют уравнениям

Z = -yI {V - а) (4.24)

(геометрическое место точек фронта) и

2 = (F - а)2; z = V (V 1){V - а) {3V - yi)-\ (4.25)

Точки пересечения кривых (4.25) представляют собой особые точки уравнения (4.18). При yi<2y+1 все эти особые точки рас-

полагаются под кривой (4.24). Используя стандартную технику качественной теории дифференциальных уравнений, которая будет детально продемонстрирована в главе 6 на другом примере, можно показать, что при таких vi найдется такое а (причем для каждой пары у, у\ только одно), что точка М (образ фронта) и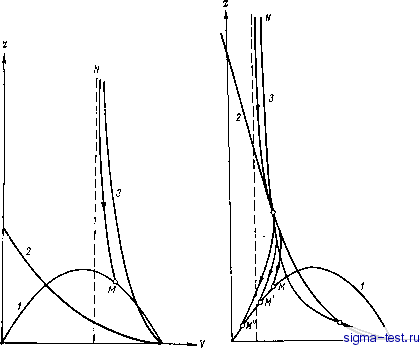

Рис. 4.4. Фазовый портрет уравнения первого порядка (4.18) при 1<yi< <2у+1.

/ - кривая (4.24): 2, 5 - кривые (4.25).

Рис. 4.5. Фазовый портрет уравнения (4.18) при yi>2y+1. обозначения см, рис. 4.4,

точка N (образ центра симметрии) будут лежать на одной интегральной кривой - сепаратрисе двух семейств интегральных кривых, единственной кривой, входящей в образ центра симметрии - особую точку типа седла уравнения (4.18). График функции a(Yi) (для у=1Д см. рис. 4.3)-монотонно возрастающая кривая, проходящая через следующие точки:

a = 2/(3Y + 2), Yi = l; = /5, Yi = 7; a = a, = (3Y + 3)/(5Y + 3), yi = 2y+1.

(4.26)

При yi>2y+1 особая точка (типа узла) располагается выше кривой (4.24) (рис. 4.5), вследствие чего получается целый интер-

вал возможных значений а. Как будет показано, при таких yi становится неединственным также решение исходной неавтомодельной задачи. Следовательно, для выделения единственного решения при таких Yi требуется дополнительное условие и в неавтомодельной задаче.

Точки (4.26) представляют специальный интерес. Первая из них соответствует движению с полной потерей тепловой энергии на фронте волны. Сжатие на фронте (отношение плотности за фронтом к исходной плотности газа) получается в этом случае бесконечным, относительная скорость газа и фронта - равной нулю. Вторая точка отвечает обычному сильному взрыву. Третья точка весьма любопытна. Она соответствует притоку энергии на фронте и выполнению так называемого условия Чепмена-Жуге: равенству скорости газа относительно фронта местной скорости звука. Действительно, скорость звука на фронте ударной волны равна

Vmlp = D /2y(yi-1)/(Yi + 1),

где D - скорость фронта. Скорость же газа относительно фронта составляет ft;/ -D = (yi - 1)/)/(yi+!) При Yi = 2y+1 эти две скорости совпадают, а поскольку а = а, образ фронта в плоскости zV совпадает с особой точкой типа узла, лежащей при этом yi на кривой (4.24). Таким образом, искомая интегральная кривая соединяет в этом случае две особые точки уравнения (4.18): сед-ловую точку (образ центра симметрии) и узел (образ фронта). Итак, при потере энергии на фронте (yi < y) и малом выделении энергии на фронте (y<Yi<2y+1) исследуемое решение мало отличается по своему характеру от решения, отвечающего обыч-. ному сильному взрыву (yi = y) особая точка типа узла располагается под геометрическим местом точек фронта, движение в возмущенной области всюду дозвуковое и т. д. При yi = 2y+1, а = а построенное решение представляет собой движение детонационного типа, но с переменной скоростью распространения фронта:

- Л37 + 3)/(5Т + 3) Г f i

На фронте волны достигается скорость звука, узел становится образом фронта. При этом приток энергии и температура на фронте оказываются зависящими от времени. Замечательно, что при Yi = 2Y-f 1 полученное решение также определяется неоднозначно. В частности, обычное решение задачи о сферической детонационной волне [40, 47], отвечающее а=1, т. е. постоянной скорости распространения волны, постоянному притоку энергии на фронте и постоянной температуре на фронте, также удовлетворяет всем условиям поставленной задачи; существует и целое семейство ре-шенийс промежуточными а: (3y + 3)/(5y+3) <а< 1.

Действительно, при yi = 2y+1 и таких а особая точка типа узла уже не совпадает с образом фронта и располагается выше