

 |
 |
|
|
Навигация
Популярное
|
Публикации «Сигма-Тест» Промежуточная асимптотика (развивающееся направление) 1 2 3 4 5 6 7 8 [ 9 ] 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 как надо выбрать определяющие параметры модели а + \у . . ., ci\ чтобы обеспечить подобие модели натуре: аГ = aL (аГ/аП\ .. {аГ/аП , (1.27) причем параметры модели а\ ..., а могут быть выбраны произвольно. Рассмотрим простые иллюстративные примеры. 1. Моделируется установившееся движение тела в безграничной вязкой несжимаемой жидкости. Тело-модель геометрически подобно телу-натуре, они отличаются только размерами; направления скоростей в модели и натуре одинаковы. Определяющими параметрами являются: характерный размер тела, например, диаметр поперечного сечения /, скорость движения У, вязкость жидкости [х, ее плотность р. Эти величины в классе MLT имеют следующие размерности: [V]LT-; [ix] = МЬ-Т ; [p] = ML-\ Таким образом, п = 4, й = 3, п - А=1, так что помимо очевидных геометрических параметров подобия имеется только один динамический П1=рУ 1. (1.28) Этот параметр был назван А. Зоммерфельдом числом Рейнольдса (общепринятое обозначение П1 = Re) в честь английского исследователя О. Рейнольдса, с исключительным успехом применившего одним из первых идеи подобия в гидродинамике. Для обеспечения подобия необходимо равенство этого параметра для модели и натуры. Аналогичная система определяющих параметров, а следовательно, и тот же динамический параметр подобия имеют место в условиях внутренней задачи, например, для течения вязкой жидкости в трубе. В этом случае за характерный размер можно принять диаметр трубы D, а в качестве характерной скорости V взять среднюю по сечению трубы скорость потока. Естественно определяются безразмерная сила сопротивления тела n = Fl±pVS (1.29) {F - сила сопротивления движению тела, SP- - площадь поперечного сечения) и безразмерный перепад давления в трубе, приходящийся на единицу длины, dp I I n = -/-f (Р/)- (1.30) На рис. 1.6 представлены зависимости этих величин от числа Рейнольдса для случаев обтекания цилиндра и движения жидкости в круглой цилиндрической гладкой трубе. Графики, построенные по данным многочисленных экспериментов, превосходно подтверждают существование для каждого случая единой зависимости П = Ф(Ке). Как видно, эти кривые имеют довольно сложный характер: участки плавного изменения П сменяются резким уменьшением или нарастанием, имеются участки на которых П почти не зависит от Re и т. д. Все это свидетельствует об изменении режимов течения с изменением числа Рейнольдса, которое представ- 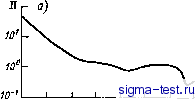 10 10 10 10 10 т iORe 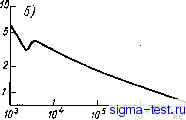 Рис. 1.6. Зависимость от числа Рейнольдса безразмерной силы сопротивления при обтекании цилиндра (а) и безразмерного перепада давления на единицу длины трубы при движении жидкости в трубе (б). ляет собой единственный параметр, определяющий глобальную структуру потока. Обычно моделирование движения тела ведется в той же жидкости, что и натурное движение. В этом случае произведения VI для модели и для натуры должны совпадать, т. е. скорость движения подобной модели растет пропорционально уменьшению размера модели по сравнению с натурой. Нетрудно показать, что силы сопротивления модели и натурного тела совпадают, так что пересчетный коэффициент равен единице. 2. По поверхности жидкости быстро движется хорошо обтекаемый корабль. Основной вклад в сопротивление быстро движущегося корабля дают создаваемые им при движении волны на поверхности жидкости. Рассматривается идеализированный случай, когда вклад вязкого сопротивления для корабля хорошо обтекаемой формы в грубом первом приближении можно считать малым. Сила сопротивления корабля F определяется его размером /, скоростью движения V, плотностью жидкости р и ускорением силы тяжести g; последний параметр существен, так как сила тяжести оказывает определяющее влияние на волны. Вхо- дящие в рассмотрение величины имеют в классе MLT следующие размерности: [F] = MLT-; [l\=L; [V\=LT-; [p] = ML; [g]=LT-, Снова n = 4, k = 3, n - k = \, и динамический параметр подобия имеет вид ni=K/V/?. (1.31) Он называется числом Фруда (общепринятое обозначение IIi = = Fr) по имени известного английского инженера-кораблестроителя В. Фруда. Таким образом,- для модели и натуры величина Vll должна быть одинаковой (параметр g можно менять лишь с большим трудом при помощи тонких ухищрений, обычно не применяемых), так что отношение скоростей модели и натуры должно быть пропорционально квадратному корню из масштаба моделирования Правило пересчета силы сопротивления с модели на натуру в той же жидкости имеет вид АР) rim)f VP\nP V .... (Р) \3 =--(-р)(Я= () т. е. сила сопротивления пропорциональна кубу масштаба моделирования. Если не пренебрегать ролью вязкости, то появится второй параметр подобия - число Рейнольдса Re = рУ 1. Моделирование с одновременным учетом обоих параметров подобия в одной и той же жидкости оказывается невозможным. Действительно, при этом требуется, чтобы для модели и натуры были равны произведения VI и отношения VIU а это возможно лишь при тождестве модели и натуры, что делает моделирование бессмысленным. В связи с этим мы ограничились для иллюстрации случаем, когда вязкое сопротивление мало по сравнению с волновым; на самом же деле вклад вязкого сопротивления моделируется отдельно от волнового при помощи специально разработанных для этой цели практических приемов. 3. Следующий пример относится к моделированию планетных атмосфер, привлекшему сейчас широкое внимание [34]. Подчеркнем, что речь идет не о моделировании конкретных течений в атмосфере той или иной планеты, а о параметрах подобия, определяющих глобальные динамические и термические свойства планетной атмосферы. Глобальные свойства планетной атмосферы определяются: 1) средней поверхностной плотностью поступающей в атмосферу за единицу времени солнечной энергии q\ 2) радиусом планеты г; 3) постоянной Стефана-Больцмана а, определяющей при заданной температуре уходящий поток излучения; 4) теплоемкостью газа планетной атмосферы при постоянном давлении Ср (газ планетной атмосферы считается термически и калорически идеальным); 5) теплоемкостью газа атмосферы при постоянном объеме
|
|
© 2010 www.sigma-test.ru Санкт-Петербург: +7 (812) 265-34-48, +7 (812) 567-94-10
Разработка и поддержка сайта: +7(495)795-01-39 после гудка 148651, sigma-test.ru(my_love_dog)r01-service.ru Копирование текстовой и графической информации разрешено при наличии ссылки. |