в стратифицированной жидкости. Следовательно, применяя преобразование Гаусса-Остроградского, получаем:

F = - J phnds - gva(i{ph)bS,

Силу сопротивления F, приходящуюся на площадку 8S проекции частицы в плане, можно вычислить следующим образом. Поскольку коллапс на рассматриваемой стадии происходит медленно, можно пренебречь ускорениями движения в пятне и упростить уравнения движения. Интегрируя эти упрощенные уравнения по толщине пятна, получаем, что сила сопротивления пропорциональна производной по Z от истинной скорости на верхней (или нижней) границе пятна. Далее, уравнения движения жидкости в пятне легко интегрируются; при этом необходимо принять то или иное граничное условие на верхней и нижней границах пятна. Эксперименты и численные расчеты показывают, что скорость на границе пятна много меньше средней скорости в пятне. Это объясняется тем, что при коллапсе вблизи пятна над и под ним происходят движения жидкости в обратном направлении по отношению к движению жидкости в пятне. Следовательно, с достаточной точностью можно считать, что на верхней и нижней границах пятна скорость обращается в нуль. Интегрируя при этом условии уравнения движения, можно получить распределение скорости по толщине пятна, а следовательно, и выражение для силы сопротивления. Мы получим это выражение непосредственно, опираясь па анализ размерности. Действительно, сила сопротивления, приходящаяся на единичную площадку, определяется местной средней скоростью жидкости v, вязкостью жидкости IX и местной толщиной пятна h. Из анализа размерности следует, что эта сила пропорциональна ixv/h. Таким образом, сила вязкого сопротивления Fr определяется соотношением

F, = cix(v/h)bS, (12.84)

где с - константа, для нахождения которой можно воспользоваться хорошо известным решением задачи о течении вязкой жидкости между плоскими стенками, согласно которому F = \2\xw8S/h, Отсюда получаем, что с= 12.

Приравнивая силу сопротивления (12.84) движущей силе интрузии частицы (12.83), получаем:

v = - {h/c\x) grad ph. (12.85)

Нам осталось найти избыточное давление в перемешанной жидкости. Распределение плотности стратифицированной жидкости по высоте вблизи уровня растекания пятна z = Zi можно считать ввиду относительно небольшой толщины пятна линейным. Ясно, что пятно растекается симметрично относительно этого уровня, так что он делит пятно по толщине пополам. Обозначим через Pi и pi соответственно давление и плотность стратифициро-

ванной жидкости на уровне z = zi. Тогда, интегрируя уравнение гидростатики, получаем, что давление в стратифицированной жидкости меняется с высотой по закону

Р = Pi - 9ig - i) + PiA {z - z,fl2. (12.86)

Здесь - по-прежнему частота Брента-Вяйсяля, так что Л2 = = agf, a=\dpldz\lpi. Таким образом, поскольку давление на поверхности пятна совпадает с давлением в окружающей стратифицированной жидкости, давления в верхней 2 = ei-f/i/2, и нижней z = Zx - /г/2 точках некоторой вертикали в пятне равны соответственно

Pu = Pi-9igh/2 + Pd=Pi+ 9igh/2 + 9,Nh/8. (12.87)

Давление внутри пятна распределено по гидростатическому закону, так как плотность жидкости в пятне постоянна и равна pi:

Р = Pi - 9ig ( - i) + PiiVVS. (12.88)

Средние давления по некоторой вертикали в пятне и такому же участку в окружающей стратифицированной жидкости равны соответственно

Pa/ = Pi+PiW8; p., = pi+piW/24. (12.89)

Разность этих величин и составляет среднее избыточное давление в пятне по данной вертикали:

Р = Рш-Ра. = Р1ВД12. (12.90)

Из соотношений (12.85) и (12.90) находим

v = - (pi/v2/12cp) h grad /г = - (piV/4cp) grad h, (12.91)

Подставляя это выражение в уравнение сохранения массы жидкости в пятне (12.82), получаем для толщины пятна нелинейное уравнение типа уравнения теплопроводности:

dth - KAh = 0; K = piN/20cii= N/20cv. (12.92)

где А = + -двумерный оператор Лапласа, v - кинематическая вязкость жидкости внутри пятна. С аналогичным уравнением мы уже встречались в главе 2 при описании начальной стадии ядерного взрыва. В частности, для плоского и осесимметрич-ного одномерных движений уравнение (12.92) принимает соответственно вид

dth-yidlxh = 0; (12.93)

dth - (и/г) дгГ drh = О, (12.94)

где X - горизонтальная декартова координата, г - горизонтальный полярный радиус.

Если начальные размеры пятна перемешанной жидкости в плане примерно одинаковы, то естественно ожидать, что пятно

становится осесимметричным уже в конце второй стадии и заведомо на вязкой стадии. На рис. 12.14 представлены результаты выполненного Е. И. Тихомировой численного интегрирования уравнения (12.92) при несимметричном начальном распределении толщины пятна h{x, у, 0). (Методы численного интегрирования уравнений типа (12.92) при вырождении - обращении h в нуль на границе возмущенной области - были развиты в работах АА. Самарского и его учеников [92, 91].) Как видно, уже при небольшом расширении форма пятна в плане становится не отличимой от круговой, поэтому в этом случае можно коллапс пятна переме-

Рис. 12.14. Численное решение уравнения (12.92) при несимметричном

начальном условии: h(x, у, 0) =ho для точек л, у внутри квадрата G; h (л:, у, 0) = О для точек вне G, выполненное

Е. И. Тихомировой.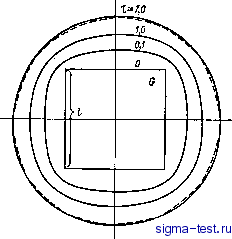

шанной жидкости считать осесимметричным и применять для его описания уравнение (12.94). Уравнение сохранения объема жидкости в пятне принимает при этом вид

2п \ h{r, t) г dr = V = const.

(12.95)

Нас интересует прежде всего промежуточно-асимптотическая стадия растекания пятна, на которой диаметр пятна в плане значительно превосходит его начальный диаметр. На этой стадии случайные детали начального распределения А (г, 0) перестают быть существенными. Следовательно, как и в главе 2, для асимптотического описания вязкой стадии коллапса пятна можно представить начальное распределение в виде сосредоточенного мгновенного источника:

/г(г, /0 = 0 при гфО; 2n\h{r, U)rdr=V,

где ti - условный момент начала вязкой стадии.

(12.96)