Через эти отверстия жидкость проникает и течет навстречу движению решетки. Из-за таких возвратных движений жидкости спустя короткое время после начала движения вблизи решетки формируется слой жидкости, имеющий толщину порядка амплитуды колебаний решетки. В этом слое жидкость совершает возвратные движения, перетекая поочередно с одной стороны решетки на другую. Основная турбулизованная область располагается ниже этого прире-шеточного слоя. Разбиение турбулизованной области на прирешеточный слой, в котором происходят возвратные движения жидкости, и основную турбулизованную область было продемонстрировано выше на рис. 12.7. Ясно, что пульсирующий прирешеточный слой передает расположенной ниже жидкости энергию, определяемую пульсационным движением на их общей границе и только им. Толщина прирешеточного слоя имеет порядок величины амплитуды колебаний решетки.

В интересующие нас времена, когда нижняя граница перемешанной области достаточно далеко ушла от решетки, можно считать, что верхняя граница основной турбулизованной области находится при г = 0. Из пульсационной энергии единицы массы можно составить единственную величину размерности потока турбулентной энергии - Действительно, s/b с точностью до постоянного множителя - средняя скорость пульсационного движения. Поэтому величина у = 6/2 ри г = 0 (снова с точностью до множителя) представляет собой средний перенос величины b пульсационным движением на единицу площади за единицу времени. Он и определяет, в согласии со сказанным, приток турбулентной энергии к турбулизованной области на ее верхней границе, т. е. при г = 0. Таким образом,

{I л/ЬдгЬ)г = о=-1ЬиО, t),

где -безразмерный множитель, который может определяться только формой ячеек решетки и ее просветностью (поверхностной пористостью). Подставляя это условие в соотношение (12.57) и учитывая нормировочное условие (12.63), получаем

(а Vrdflct)i==o= -I If (0)]/ = -1,

откуда находим

f{0) = (\/X)

Решение уравнения (12.58), удовлетворяющее условиям (12.50), непрерывное и имеющее непрерывную величину л/fdfldl, определяется единственным образом и при произвольном \1 предыдущему соотношению не удовлетворяет. Существует, однако, исключительное значение параметра ц - собственное значение - при котором это условие удовлетворяется; оно и определяет искомое решение.

Отметим, что пока неясно, как практически задавать параметр по заданной форме решетки, поэтому само собственное значение \i может оказаться непосредственной характеристикой формы решетки.

7. Продемонстрируем постановку и решение задачи на собственные значения для близкого явления распространения турбулентности от мгновенного источника, представляющего также самостоятельный интерес.

Пусть в безграничном пространстве, заполненном несжимаемой однородной жидкостью, в начальный момент = О создается плоский турбулентный слой постоянной толщины 2а, в котором распределение турбулентности симметрично относительно горизонтальной плоскости 2 = 0 и горизонтально однородно. В последующие моменты времени слой расширяется в вертикальном направлении, захватывая окружающую жидкость.

Таким образом, начальное условие для распределения турбулентной энергии имеет вид

b{z, 0) = {Q/a)uo(z/a),

где Uo - четная безразмерная функция своего безразмерного аргумента, равная нулю при \z\la\, а величина Q - интенсивность мгновенного источника турбулентности, приходяш.аяся на единицу площади границы слоя:

Q= \ b{z, 0)dz.

Вполне аналогично предыдущему можно показать, что при больших временах асимптотика решения поставленной таким образом задачи представляется в виде (12.57), где

Л = д(1-)/узц-1)/2

причем полутолщина hit) турбулизованного слоя в момент t определяется соотношением (12.59). На границах слоя z=±h{t) турбулентная энергия и ее поток обращаются в нуль. Таким обра-, зом, интегрируя уравнение (12.58) по I от -о до о, получаем:

(12.64)

Из этого соотношения следует, что 1>7з. Из условия расширения слоя находим (ср. (12.59)), что i<l. Таким образом, если устремить начальную толщину слоя а к нулю, то для сохранения неизменной асимптотики решения при больших временах интенсивность источника должна возрастать и притом так (ср. главу 3), чтобы оставался неизменным момент Qa~~\ Полагая для удобства Z = l/h = zlh{t), Ф() = g~f, приведем уравнение (12.58) к виду

(d/dt,) (ал/Ф dФ/dO + (1 ~ х) С dO/d! + 2iO - сфУа = 0. (12.65)

Ввиду симметрии задачи Ф(=Ф(-g), и можно ограничиться построением решения только при gO. Таким образом, ищется нетривиальное решение уравнения (12.65) в интервале О = 1, удовлетворяющее условиям

ЙФ(0)/ЙС = 0; Ф(1) = 0, (12.66)

непрерывное и обладающее непрерывной производной dO/dt,. Из непрерывности этой производной вытекает, в частности, условие

dO (l)ldI = 0, (12.67)

которому искомое решение также должно удовлетворять.

при малых Ф последний член уравнения (12.65) мал сравнительно с предыдуш.им и может быть отброшен. Легко показать, что получаюш,ееся при этом уравнение инвариантно относительно группы преобразований

где А, > О -параметр группы. Следовательно, порядок уравнения можно понизить до первого и оно может быть исследовано (ср. [4, 17]). Исследование показывает, что нетривиальное решение уравнения (12.65), обладающее нужной гладкостью и удовлетворяющее условиям Ф(1) =0, Ф/2(1)/й =0 существует и опреде-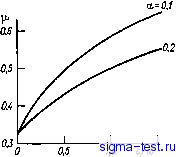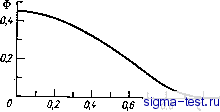

Рис. 12.9. Зависимость параметра \i от параметров задачи а и с/а.

Рис. 12.10. Универсальное распределение турбулентной энергии по толщине слоя при а=0,2 и с/а=0,5.

ляется единственным образом; для него при 1 справедливо разложение

Ф = [(1 - р)/2а]2 (1 С) - [(1 - Р)М (1 )3 + . . .

Однако при произвольном р оставшееся условие йФ(0)/ = = О не выполняется. Мы пришли, таким образом, к классической ситуации нелинейной задачи на собственные значения: нужно построить нетривиальное решение уравнения (12.65), удовлетворяющее условиям (12.66), (12.67) и имеющее нужную гладкость, и определить значение параметра р, для которого такое решение существует. Можно показать, что решение этой задачи существует и единственно; она легко решается численно. Результаты определения р для разных значений параметров а и с/а представлены на графике рис. 12.9. Решение Ф() для случая а = 0,2 и с/а = = 0,5 представлено на рис. 12.10.

Вычисления выполнены Е. С. Бениловым.