шетки с Vp/t/ = 3 и 0,35 для подвижной решетки с Vp/U= 17, Этот показатель зависит, таким образом, от начальных условий, т. е. условий на решетке.

Работа Гад-эль-Хак и Коррсина [128] содержит результаты обработки данных других, как правило, с нашей точки зрения менее совершенных, экспериментов различных авторов. Обработка велась по зависимости величины Bll(0, t) от t, зависимость предполагалась, согласно (10.27), степенной. В некоторых случаях турбулентность была слабо анизотропной, поэтому в работе [128] приведены показатели затухания всех трех компонентов пульсационной скорости. Эксперименты, как правило, проводились на пассивных решетках, за исключением некоторых опытов, о которых сообщается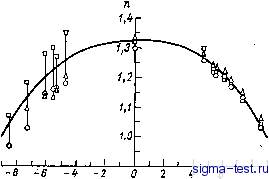

Рис. 10.8. Зависимость показателей степени в законе затухания Bll(0, t) за активной решеткой от относительного расхода / воздуха для различных компонентов скорости [128].

При вдуве по потоку />0, против потока /<0. При />0 затухание изотропно, показатель степени отличается от единицы.

В той же работе [128}. В этих опытах, как уже говорилось выше, использовалась решетка из полых стержней с соплами, через которые в поток подавался воздух. Зависимость показателей степени в законе затухания Bll(0, t) за активной решеткой от относительного расхода / воздуха, подаваемого через сопла решетки, представлена на рис. 10.8.

Как оказалось, показатели степени в законе вырождения зависят от условий на решетке (число Рейнольдса решетки, характеристики ее активности: /, Vp/U, со и т. д.). Показатель а оказался равным нулю, т. е. автомодельность вырождения оказалась полной только в случае чудовищно больших чисел Рейнольдса решетки, полученных в работе Кистлера и Вребаловича [152].

К сожалению, третьи моменты почти никем не измерялись: одной из немногих работ, в которых измерялись третьи моменты, остается на сегодня работа Стюарта [195]. В ней подтверждается автомодельность коэффициента корреляции и обращается внимание на отсутствие единой зависимости отношения Вьь,ь{Гу t)IB{Q, t) от автомодельной переменной для разных

моментов времени (рис. 10.9). Это согласуется с неполной автомодельностью вырождения (см. (10.26)) и не должно иметь места при полной автомодельности.

Итак, мы приходим к выводу, что в опытах уже на небольших расстояниях от решетки вырождение турбулентности автомодельно, причем эта автомодельность неполная, так что влияние начального размера (размера решетки) не исчезает никогда, но благодаря особенностям изотропной однородной турбулентности проявляется только в комплексе с другими параметрами. Показатель степени в законе вырождения не может быть определен из соображений анализа размерностей, но выделяется из непрерывного

Рис. 10.9. Зависимость величины Bii,i(r,0/4i(0, t) от автомодельной переменной g [195].

Кривые для разных моментов времени не совпадают. /) /=0.041 с; 2) /=0,0615 с; 3) /=0,123 с; 4) /=0,184 с: 5) /=0,246 с.

спектра возможных значений начальными условиями (условиями на решетке) -ситуация, в принципе аналогичная той, с которой мы столкнулись выше при рассмотрении автомодельного аналога уравнения Кортевега-де Фриза.

Сделанные выводы, разумеется, относятся только к случаю слабой турбулентности, для которой значения ReT = vl/v (v- масштаб пульсаций скорости, / - линейный масштаб турбулентности) достаточно малы. В противном случае нет оснований ожидать независимости от Rer, т. е. автомодельности вырождения.

Изложенный выше анализ автомодельного вырождения однородной изотропной турбулентности был выполнен в работе [15].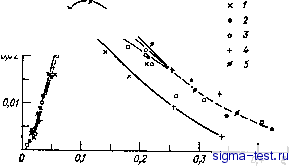

10.5. Локально-изотропная турбулентность

Исследование локальной структуры турбулентных течений несжимаемой вязкой жидкости при больших числах Рейнольдса в замечательных работах А. И. Колмогорова [54, 155] и А. М. Обухова [79, 173] также доставляет показательные примеры автомодельных промежуточных асимптотик различных типов. Здесь следует отметить также выдающуюся работу их предшественника Л. Ф. Ричардсона [186], предложившего качественную картину вихревого каскада в турбулентном потоке.

Согласно основному предположению А. И. Колмогорова, при больших числах Рейнольдса гидродинамические поля обладают свойством локальной изотропии, однородности и стационарности.

Локальная изотропия и однородность означают, что тензоры моментов, в которые входят относительные скорости

ArU = u(x + r, 0-u(x, /), (10.28)

при достаточно малых г изотропны и однородны. Условие стационарности статистических характеристик локальных полей объясняется тем, что характерные времена мелкомасштабных локальных полей много меньше характерных времен изменения основного потока.

Таким образом, как и в случае обычной изотропии и однородности турбулентного потока, тензор вторых моментов величин Аг U выражается через один из своих компонентов, например,

DLL = <{uL{x + r, t)-u,(x, t)f), (10.29)

где Wl-компонент вектора скорости и по направлению г. Величина Dll зависит от г - модуля вектора г, а также от кинематической вязкости жидкости V, внешнего масштаба Л и некоторого параметра, определяющего интенсивность турбулентности. В качестве такого параметра удобно принять среднюю энергию, передаваемую за единицу времени рассматриваемым мелкомасштабным движениям от крупномасштабных, которая в силу стационарности равна в расчете на единицу массы средней скорости вязкой диссипации энергии <8>. Величина <е> имеет, очевидно, размерность L?-. Удобно ввести в рассмотрение вместо вязкости линейный масштаб X движений, на которых происходит вязкая диссипация, определяемый величинами v и <8>, согласно анализу размерностей, соотношением

;, = v/V8r/\ (10.30)

Этот масштаб называется колмогоровским внутренним масштабом. Таким образом, получаем

DLL = f{r. <8>, я, Л). (10.31)

Анализ размерностей дает по стандартной процедуре

Dll = <8УУ/Ф (г/Я, г/Л). (10.32)

Закономерности, справедливые в так называемом инерционном интервале масштабов, много меньших внешнего и много больших внутреннего, т. е. при Я<г<Л, представляют собой промежуточную асимптотику (10.32) при г/Я->сю, но г/Л->0 (при больших числах Рейнольдса, очевидно, %{{{А). В классическом варианте теории Колмогорова-Обухова делается предположение, равносильное предположению о полной автомодельности по обоим параметрам гIX и г/Л, так что при Хг<А получается закон двух третей Колмогорова-Обухова;

011 = Сфг\ (10.33)

где с - универсальная постоянная, которая должна быть равна

Ф(СХ), 0).