Л = Ло. Л. Г. Лойцянский [65] показал, что при определенных предположениях эта величина не изменяется во времени и при учете третьих моментов.

Можно показать, используя свойства конфлюентной гипергеометрической функции, что решения (10.10) с А1>2 обладают интегралом Л, равным нулю. Эти решения в определенном смысле неустойчивы по отношению к начальным данным. Действительно, если возмущения такого решения обладают пусть малым, но конечным Ло, то при достаточно больших временах именно вклад возмущения будет определять закон затухания, поскольку он соответствует меньшему /г, а именно п = V2. По этой причине автомодельные решения с /г>2 представляют меньший интерес. Напротив, представляют существенный интерес решения с п<2, для которых Ло = оо. Эти решения можно записать в виде

Вы {г, t) = (Ло/ Vv {t - tof) (Vv {t - o) ) / Mv {t - 0), ai),

(10.17)

где Ло и / - постоянные, имеющие соответственно размерность и L, причем эти постоянные выбраны так, что А = =Ао1--\-. Как видно, все решения с пф12 представляют собой автомодельности второго рода, запомнившие характерный размер начального распределения / (ср. главу 3, где на примере другой задачи разобрана вполне аналогичная ситуация). Дело в том, что асимптотика безразмерной функции Oll(I, Л )

где l = r/v{t - 0), Ц = 11л/{1 - о), появляющейся при применении анализа размерностей к решению Вьь{г, t) исходной неавтомодельной задачи, имеет при малых ц вид

Ф (, Л, ...)Л-Ф111(Н, ...).

Таким образом, характерный размер начального распределения / хотя и входит в определяющую решение константу Л, но только в комбинации с Ло, и поэтому не портит автомодельности.

Заметим, что стадию развития изотропной однородной турбулентности, на которой третьи моменты пренебрежимо малы, иногда называют заключительной стадией вырождения. Это аргументируется тем, что на заключительной стадии малы скорости, и, следовательно, третьи моменты, имеющие порядок куба скорости, малы по сравнению со вторыми, имеющими порядок квадрата скорости. Такая аргументация на самом деле недостаточна, потому что третьи моменты входят в основное уравнение Кармана-Хауэрза (10.8) с производной на единицу меньшего порядка, чем вторые, а каждое дифференцирование повышает скорость вырождения соответствующего члена. В действительности, стадия, на которой третьи моменты пренебрежимо малы, может иметь место лишь в начале движения при специальном выборе начальных условий.

10.4. Вырождение изотропной однородной турбулентности при конечных третьих моментах

С самого возникновения в работах Дж. И. Тейлора [200] представления об изотропном однородном турбулентном потоке его пытались моделировать затуханием турбулентности в аэродинамических и гидродинамических трубах. Подробная сводка этих работ имеется в статье Гад-эль-Хак и Коррсина [128]. Следует специально отметить исключительные по тщательности эксперименты, выполненные Лингом с сотрудниками [162, 163] в гидродинамической трубе - длинном канале квадратного сечения, в который подавалась вода через пассивную или активную решетку стержней.

+ i i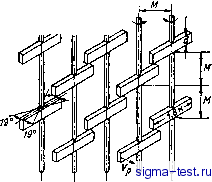

Рис. 10.1. Турбулизирующие решетки, использованные в работах [162, 163]: пассивная (а) и активная (б).

На рис. 10.1 приведены схемы решеток, использованных в этих работах. В активной решетке стержни были снабжены лопатками, совершающими колебательное движение с различной скоростью. В работе Гад-эль-Хак и Коррсина [128] использовались другие активные решетки, стержни которых были полыми, а сопла направлены по потоку или против потока. Через полые стержни и сопла в поток подавался воздух (в этой работе исследование проводилось в аэродинамической трубе) с различным расходом.

Таким образом, во всех этих опытах турбулентные возмущения вносятся в поток на решетке и затем затухают по мере продвижения по потоку. При этом пульсации скорости уже на небольших расстояниях от решеток становятся близкими к изотропным. На рис. 10.2 изображены результаты измерения отношения средних квадратов пульсаций продольной и поперечной компонент скорости [162]. Как видно, эти отношения близки к единице. Ясно, что если принять за время величину t = x/U (f/ -средняя скорость подводимого к решетке потока, х - координата, отсчитываемая вдоль канала от решетки), то картина затухания турбулентности по мере продвижения вдоль канала достаточно хорошо соответ-

ствует схеме вырождения изотропной однородной турбулентности во времени (однородность также проверялась специально путем перемещения по сечению х = const датчиков, при помощи которых производились измерения скорости).

Статистические характеристики - моменты рассматриваемого турбулентного движения -определяются, таким образом, средней скоростью подводимого к решетке потока (/, характерным размером решетки Л1, толщиной стержней d, коэффициентом вязкости v и величинами г и i - о, где - эффективное начало отсчета времени, об определении которого будет сказано ниже. Далее, для активных решеток, подобных тем, что были использованы Лингом и Ваном 163], моменты определяются также скоростью Ур и ча-

1,0 0,9,

0 80 120 160 200 20 280 х/М

Рис. 10.2. Пульсации скорости в турбулентном потоке за решеткой [162].

/) Кед,-470. Л1-1.78 см. M/rf=2,8. U2,9 см/с; 2) Ref-940. М--3,56 см, M/d=2.8. 6=2.9 см/с; 3) Ref 840. Л1-3.18 см, M/cf=5,0. £/=2,9 см/с.

стотой 0) колебаний концов лопаток; для активных решеток, использованных в работе Гад-эль-Хака и Коррсина [128], дополнительным определяющим параметром моментов является относительный расход газа через решетку J = QJQ (Qi -расход газа, подаваемого через полые стержни решетки; Q -расход газа, подаваемого к решетке).

Из анализа размерности для двухточечных моментов второго и третьего порядка получаем

Вы = Ь/ИЩФы{1. Mid, MU/v, ...); (10.18)

BLL,L = \y/{t-to)f0 ,i{l, л> M/d, MU/v, ...), (10.19)

где Ф с индексами - безразмерные функции своих безразмерных аргументов

E = r/Vv(-/o); n = M/U{tto),

параметра решетки M/d, числа Рейнольдса решетки MU/v, а также параметров, характеризующих активность решетки.

Представляет интерес рассмотрение движения на достаточно больших удалениях от решетки, где i[] = M/U{t-to)<l и можно