Во втором случае соотношение (7) при малых (больших) Пи П2, .. . можно переписать, используя (25), в виде

n* = Oi(n**, Пз, ...); п* = ппГ; п** = П2ПГ (26)

Таким образом, и в этом случае число аргументов зависимости (7) уменьшается. Параметры П* и П** вполне аналогичны по своей структуре обычным параметрам подобия - это степенные комбинации определяемых и определяюидих параметров. Разница состоит, однако, в том, что, во-первых, величины П*, П** содержат размерные параметры dk+u портившие автомодельность исходной задачи, и, во-вторых, они не могут быть получены анализом размерности. Примером таких параметров является в модифицированной задаче теплопроводности величина

В ней содержится размер области начального тепловыделения I в степени а, которую нельзя определить из соображений размерности. В случаях, подобных рассматриваемому, говорят о неполной автомодельности по параметрам 111, П2, ...

Наконец, в третьем случае параметры П1, П2, ... продолжают оставаться существенными, как бы велики или малы они ни были, и никакая автомодельность по ним не наступает. Природа классификации автомодельных решений теперь становится прозрачной. Если предельный переход от решения неавтомодельной исходной задачи к автомодельной промежуточной асимптотике отвечает полной автомодельности по безразмерному параметру, нарушающему автомодельность исходной задачи, автомодельное решение представляет собой решение первого рода. Если предельный переход соответствует неполной автомодельности, автомодельное решение является решением второго рода. Трудность на самом деле состоит в том, что методы подобия обычно применяются, когда решение полной задачи неизвестно. Поэтому априори нельзя указать, с каким типом автомодельности мы имеем дело и практически поступают так: сначала предполагают полную автомодельность и пробуют построить соответствующее автомодельное решение - решение первого рода. Если это предположение приводит к противоречию, то возвращаются к исходной невырожденной задаче, предполагают неполную автомодельность и пробуют построить автомодельное решение второго рода. Если и это предположение приводит к противоречию, автомодельность вообще не имеет места.

8. Поучительные примеры автомодельных решений второго рода доставляют решения даже таких простых и общеизвестных задач, как плоское течение идеальной несжимаемой жидкости в углах. Проиллюстрируем указанный выше подход на одной такой простой задаче. Выясним поведение плоского течения идеальной несжимаемой жидкости, возникающего при обтекании поступательным потоком клина, вблизи острия клина. Предположим сначала, что продольный размер клина L несуществен, так как

его отношение к расстоянию от острия г очень велико, и попытаемся построить, используя метод анализа размерностей, автомодельное решение первого рода -решение задачи обтекания бесконечного клина с углом раствора 2а потоком со скоростью U на бесконечности (рис. 1 а). Очевидно, что течение потенциально, v=grad9 и потенциал ф может зависеть только от следуюидих величин: f/, г, 0, а. Здесь г, 0 -полярные координаты с центром в вершине клина. Анализ размерностей приводит по указанной выше процедуре к соотношению ф = [/гФ(0, а).

Из уравнения неразрывности для несжимаемой жидкости divv = 0 и потенциальности поля скорости получим уравнение Лапласа для потенциала

Аф = г~дгГдгЦ) + г сееф = 0.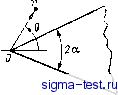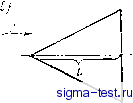

Рис. 1. Обтекание клина идеальной несжимаемой жидкостью.

а - бесконечный клин, б - клин конечных размеров.

Подставляя в это уравнение соотношение ф = [/гФ(0, а), можно легко получить, что Ф = Л cos 0 + 5 sin 0. Таким образом ф оказывается равным потенциалу поступательного потока: ф = = Лх + 5г/, который, очевидно, не удовлетворяет условиям на боковых сторонах клина: получилось явное противоречие. Для разрешения противоречия обратимся по указанному выше правилу к невырожденной задаче обтекания плоским потоком идеальной жидкости клина конечных размеров (рис. 1 б). В этом случае решение заведомо существует, но среди определяющих параметров появляется еще один - размер клина L, и решение перестает быть автомодельным. В самом деле, анализ размерности дает

ф = [/гФ(т1, 0, а); ц = г/Ь. (27)

Предположение о полной автомодельности по г], т. е. о существовании конечного предела решения при L-oo - решения задачи для бесконечного клина, оказалось неправильным. На самом деле имеет место неполная автомодельность по г], т. е. существует такое ХФО, что Ф (ц, 0, а) = г]Ф1(0, а) при малых г]. Отсюда следует, что при малых г], т. е. вблизи вершины клина, или при увеличении размера клина L предельное выражение для потенциала ф имеет вид ф = f/L-r+Фl (0, а). Подставляя это выражение в уравнение Лапласа и решая его, получаем:

= Аг+ cos [{к + 1)0+y1, (28)

где А =UL~; Р, у - безразмерные постоянные. Собственное значение к определяется из условия существования автомодельного решения в целом, в данном случае из условия обращения в нуль окружной компоненты скорости на щеках клина 9 = а и 9 = 2я - а, линии симметрии 9 = я, и только на этих линиях. Отсюда находим Х = а/(я -а), у =-п/(п -а). Константа р может быть найдена сращиванием с решением исходной невырожденной задачи, которое без труда получается применением конформного отображения. Мы построили автомодельное решение второго рода, представляющее асимптотику поля потока вблизи вершины клина. Заметим, что ставя задачу обтекания бесконечного клина, мы на самом деле интересовались именно этой асимптотикой!

Приведенный здесь пример достаточно прост, чтобы можно было построить полное решение невырожденной задачи. Вместе с тем он ясно показывает те сложности, которые могут появиться в тяжелых нелинейных задачах, когда решение невырожденных задач недоступно.

9. Выяснению природы автомодельностей второго рода помогло установление тесной связи классификации автомодельностей и нелинейных бегущих волн [19, 109]. Бегущие волны представляют собой решения вида

u = f{l;lx + c). (29)

Здесь Z и т - пространственная и временная переменные, К - постоянная скорость распространения волны, с - константа. Для таких решений распределения характеристик в разные моменты времени получаются одно из другого простым сдвигом. Хорошо известно, что бегущие волны подразделяются на два типа. Для волн первого типа скорость распространения К находится только из законов сохранения и не зависит от внутренней структуры волны. Примером таких волн являются ударные волны в газодинамике и детонационные волны. Для волн другого типа скорость распространения К находится из условия существования в целом решения, описывающего внутреннюю структуру волны, и полностью этой структурой определяется. Примером волн этого типа является волна пламени или волна распространения гена, имеющего преимущество в борьбе за существование. Следует отметить, что рассмотрение последней задачи в классической работе А. И. Колмогорова, И. Г. Петровского и И. С. Пискунова [54] было первым примером строгого анализа промежуточной асимптотики нелинейных задач.

Положим теперь в выражении (29) = lnx; т = 1п/; с = = -In Л. Тогда это выражение преобразуется к автомодельному

ЛУ f(lr + c) = f (In (x/At)) = F (x/AP). (30)

Этим преобразованием разделение автомодельных решений на решения первого и второго рода ставится в однозначное соответствие классификации бегущих волн, о которой было сказано выше.