Условия на фронте (4.2), (4.3) так же, как и в обычной задаче о сильном взрыве (глава 2), приводятся к виду

Pf=9.D- Щ = -П; а, = -р . (4.4)

Уравнения движения газа в области непрерывного движения также остаются неизменными:

dtv -\-vdrV + drpip = 0; dtp + dr {pv) + 2pvlr = 0;

dt{pm + vdr{p/p) = 0. (4.5)

Сохраняет свою форму и условие отсутствия притока вещества и энергии в центре взрыва при / > 0:

v{0, 0 = 0. (4.6)

Мы получили, таким образом, почти ту же задачу, что и раньше, с той, однако, разницей, что показатели адиабаты в условиях на фронте ударной волны и в уравнениях движения газа в непрерывной области различны.

4.2. Прямое применение анализа размерности

в модифицированной задаче о точечном сильном взрыве

Попробуем теперь построить такое же, как и ранее, автомодельное решение этой задачи, отвечающее мгновенному выделению в точке -центре взрыва - конечной порции энергии Е. Казалось бы, ничто в наших рассуждениях не должно измениться. Действительно, единственным новым определяющим параметром в рассматриваемой нами задаче по сравнению с обычной задачей о сильном взрыве является постоянный безразмерный параметр yi. так что соображения анализа размерности остаются прежними, и искомое решение должно, на первый взгляд, по тем же причинам, что и в главе 2, представляться в виде

P = Po(г7)P(c, y/yi); Р = Ро/?(, Y, Yi); v = {rlt)V {l, у, у,);

t = г (Et/роУ; п (О = 0 (Y, Yi) (Е/роУ\ (4.7)

Функции Р, Vy R должны удовлетворять той же системе обыкновенных уравнений, что и в обычной задаче о сильном взрыве, поскольку уравнения движения газа в области непрерывного движения не изменились и по существу той же осталась форма автомодельного решения, которое мы ищем.

Далее, в силу (4.7), D = drf/dt = 2rf/5t, Подставляя в (4.4) остальные выражения (4.7), получаем:

P{h. Y, Yi)=8/25(Yi + l); Y, Yi) = (Yi + 1)/(Yi ~ 1);

(0, Y, Yi) = 4/5(Yi + l). (4.8)

Эти выражения - граничные значения функций Р, F, R на фронте g = go - отличаются от соответствующих граничных значений для случая обычного сильного взрыва (2.26) только тем, что вместо показателя адиабаты у в них входит yi-

Однако решения нашей новой задачи, имеющего форму (4.7), при Yi=7y в разумном классе функций не существует. Для того чтобы в этом убедиться, заметим, что если бы решение имело форму (4.7), то полная энергия газа в возмущенной области S была бы постоянна, что доказывается точно так же, как и раньше (см. соотношение (2.27)). Однако при Yiy полная энергия газа в возмущенной области должна изменяться за счет потерь или притока энергии на фронте волны:

dS/dt = -Anrfpf {Vf - D) Б =

= ~4ягр {Vf D) (Yi - y) Pf/(Yi - 1) (y - 1) Pf = 0. (4.9)

Получившееся противоречие доказывает несуществование решения нашей задачи, имеющего форму (4.7) при yi Ф y-

4.3. Численный эксперимент. Автомодельная промежуточная асимптотика

Для того чтобы разобраться в возникшем противоречии, снова, как и в аналогичной ситуации, описанной в предыдущей главе, отступим от строгой формулировки вырожденной автомодельной задачи. Вспомним, что решение, отвечающее точечному взрыву, имеет смысл, если оно представляет собой асимптотику для решения, отвечающего выделению энергии в малой, но конечной области. Обратимся поэтому к рассмотрению задачи, в которой энергия в момент / = 0 выделяется не в точке, а в сфере радиусом /?о. В остальном же задачи совпадают. По этим соображениям в поставленном численном эксперименте решалась следующая задача. Имеется безграничное пространство, заполненное газом. В начальный момент вне сферы радиуса Rq плотность газа постоянна и равна ро, давление равно нулю. Внутри же сферы распределение характеристик движения газа (давления р, скорости V и плотности р) соответствует решению обычной задачи о сильном взрыве при энергии взрыва Е и тех же значениях прочих параметров в некоторый момент 1 = и после взрыва, отвечающий достижению ударной волной радиуса Rq. Таким образом, считалось, что при -0 <0 происходит обычный сильный взрыв без излучения и выделения энергии на фронте, а при t = О включается излучение или выделение энергии на фронте. При дальнейшей эволюции движения характеристики потока в области непрерывного движения описываются системой уравнений адиабатического движения газа (4.5). На фронте ударной волны условия имеют вид (4.4). Это те же условия, что и в обычной задаче о сильном взрыве; однако подчеркнем еще раз, эффективный показатель

адиабаты у\ в условиях на фронте отличается от показателя адиабаты Y в области непрерывного движения, фигурирующего в уравнении сохранения энтропии. Кроме того, выполняется условие отсутствия притока вещества и энергии в центре взрыва при > О,

Рис. 4.1. Зависимости 1пг/(0, ln(t)y полученные численным счетом неавтомодельной задачи.

Результаты численного расчета представлены на рисунках 4.1 и 4.2, а также в табл. 4.1. Вычисления проводились для двух зна-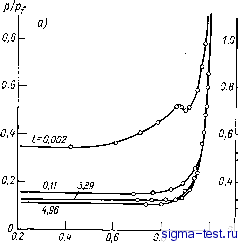

p/Pf

1=0,00081

1,0 0,2

0,000089

0,0188(0,219) 0,000069

0,6 0,8 r/Vf(t)

Рис. 4.2. Зависимости р/р/ от г/г/, полученные численным счетом неавтомодельной задачи.

а) Y=I,9, Yi=l.l; б) у=1Л, Yi = l,9.

чений y: значения, близкого к единице (y = 1,1), и значения, близкого к двум (y= 1,9). В каждом случае расчеты проделаны для нескольких значений yi в интервале 1 =Yi 2Y-f 1. Наряду с величинами р, р, V, ff считалась также суммарная энергия газа в возмущенной области . Основной результат заключается в том,