откуда и из (6.29) получаем граничные условия для функции P(f/, X):

р = 0, U = uu р = 0, U = U2. (6.38)

6.4. Нелинейная задача на собственные значения

Мы снова, как и в случае автомодельных решений второго рода, получили нелинейную задачу на собственные значения: уравнение (6.36) - уравнение первого порядка, в то время как граничных же условий (6.38) два. Покажем, следуя Я. Б. Зельдовичу [41], что имеется, и притом единственное, собственное зна-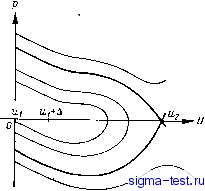

Рис. 6.3. Фазовый портрет уравнения первого порядка (6.36).

чение Я = Ко, для которого сушествует искомое решение. Рассмотрим фазовый портрет уравнения (6.36) в интересующей нас области плоскости Up (рис. 6.3). При U = U2, р = 0 уравнение (6.36) имеет особую точку типа седла. Через эту точку проходят

две сепаратрисы с наклонами -Я/2±уЯ2/4 - 4{u2); поскольку 42) <0, наклон одной из сепаратрис положительный, другой-отрицательный. Ясно, что удовлетворить второму условию (6.38) могут только сепаратрисы. Далее, при 1 = 0 уравнение (6.36) интегрируется в конечном виде: решения, удовлетворяющие условию (6.38) при и = U2 имеют вид

р = ±д/2 ] iu) du.

(6.39)

так что ординаты точек пересечения соответствующих интегральных кривых с осью ординат равны соответственно

p=/J2\w{u)du>Q\ p2 = -\/2\w{u)du<0. (6.40)

Рассмотрим теперь функцию q{U, %) = дхр для всех решений уравнения (6.36), удовлетворяющих второму условию (6.38). Ясно, что q{u2y Х) =0, поскольку p{u2, Х)=0. Дифференцируя (6.36), получаем для функции q уравнение

dqIdU = l+W(U) qlp, (6.41)

Вблизи точки и = U2 сепаратрисы ведут себя, согласно предыдущему, как

Р = (f/ - U2) (-4- ± л/т - (%)).

Дифференцируя по К находим, что соответствующие кривые q{U, К) вблизи и = U2 ведут себя, как q = K{U - W2), где коэффициент

К = {-V2 ± Я/2 - {U2)}

отрицателен для обеих сепаратрис, т. е. > О при U < U2. Далее, кривые q (С/, X) не могут пересечь ось q = 0 в некоторой промежуточной между Ui и U2 точке, так как в точке пересечения выполнялось бы соотношение dqIdU = -\, что геометрически невозможно. Таким образом, 9(/1+А, Я) > 0. Однако Ч([/)=0 при u\uu\+/S., откуда и из (6.41) получаем q{u\,%) = = (ti+А, А) + А >А. Поскольку

p{uu X) = p{uu 0) + \q{uu K)dl>-yy 2 \w{u)du + lA,

(6.42)

TO, следовательно, найдется такое Я = Яо и притом только одно, что нижняя сепаратриса войдет в точку р = О, U = uu т. е. удовлетворит всем условиям задачи.

Итак, существование и единственность решения нелинейной задачи на собственные значения доказаны. Используя методы, )азвитые в работе А. Н. Колмогорова, И. Г. Петровского и Т. С. Пискунова [57], Я.И. Капель [50] показал, что решение представляет собой асимптотику при too решения некоторого естественным образом определенного класса начальных задач с условиями переходного типа. Заметим, что как в задаче о распространении гена, так и в задаче теории распространения пламени, непосредственное построение решения типа бегущей волны u = U{l - Ы + с) определяет это решение с точностью до константы с. Эта константа может быть найдена только сращиванием инвариантного решения с неинвариантным решением исходной задачи. При этом очевидно, что какое бы промежуточное состояние системы 1/(1, и{1, й), п{1, &) мы ни приняли за начальное, значение константы с не изменится. В этом смысле константа с является интегралом уравнений рассматриваемых задач (ср. [159]).

Полученное собственное значение Ко и определяет, если возвратиться к исходным размерным переменным, скорость распространения пламени:

m = XoDh. (&.43)

Далее, поскольку в задаче определения скорости бегущей волны фигурировало быстрое время, ясно, что на самом деле, в естественном внешнем масштабе времени выход на асимптотику происходит весьма быстро и доасимптотическая эволюция решения на самом деле не имеет значения.

6.5. Распространение пламени по реагирующей смеси - промежуточная асимптотика

В предыдущем изложении мы предположили, что химическая реакция в смеси при начальной температуре не идет: Ф(п, ui) = = 0. Более того, мы дополнительно потребовали выполнения сильного и несколько искусственного, на первый взгляд, условия обращения скорости реакции в нуль также в некотором интервале температур: Ф(п, и)=0, Uiu Ui + A. В то же время в физической химии для скорости реакции обычно принимается аррениусовская зависимость

Ф(/г, u)=AnPexp{-EIRu), (6.44)

где постоянные Л, р - предэкспонент и порядок реакции; постоянная Е - теплота активации химической реакции; R - универсальная газовая постоянная. Зависимость (6,44) дает для практически встречающихся начальных температур смеси хотя и очень малые, но все же отличные от нуля значения скорости реакции. Значит ли это, что решения нелинейной задачи на собственные значения тео-. рии распространения пламени не существует и промежуточной асимптотики типа бегущей волны в этой задаче нет?

На самом деле оба наложенных выше на скорость реакции условия не необходимы. Достаточно, чтобы скорость реакции при исходной температуре была бы много меньше максимальной для данного процесса скорости реакции. При этом промежуточной асимптотикой распределения температуры, концентрации горючего вещества и т. п. по-прежнему будет некоторое решение типа бегущей волны- распространяющееся пламя.

Покажем это. Для упрощения изложения сделаем некоторые непринципиальные предположения. Примем, во-первых, что закон подобия полей концентрации и температуры Льюиса-Эльбе имеет место и на стадии нестационарного распространения пламени:

Qn/o + u = U2 = const, (6.45)

где U2, по-прежнему, постоянная температура сгоревшей смеси. Далее, пренебрежем расширением газа при сгорании и возникаю-