конечен, отличен от нуля и сохраняется во времени, если интеграл

J и°Ф(£. e)dl (3.16)

- со

конечен и отличен от нуля. Само решение (3.14) отвечает сингулярным начальным данным, однако эта сингулярность уже не есть классическая б-функция, как в случае 8=1.

Функцию Ф(, е) удобно нормировать следующим образом:

Ф(0, 8) = 1, (3.17)

при этом выполняется соотношение а (О, t) = A(>it)~-.

Подставляя (3.14) в основное уравнение (3.1), получаем для функции Ф(, 8) обыкновенное уравнение с разрывным коэффициентом при старшей производной:

+ 4- + -ЦФ = 0 при 0<<Ь;

, 1 , , l + cLф o прио<&<оо. (3.18)

2

Здесь о - точка, в которой обращается в нуль производная dO/flfl, или, что в силу (3.18) то же, выполняется соотношение

£+(1+а)Ф = 0. (3.19)

В самом деле, левой части этого соотношения пропорциональна производная дш. Функция Ф(5, г) в силу естественной симметрии решения -четная. Вследствие отсутствия притока при л: = Ов моменты t>0 справедливо граничное условие

Ф =0. (3.20)

Кроме того, функция Ф(, е) и ее первая производная по-g должны быть непрерывны повсюду, и в частности при = (напомним, что это вытекает из того, что давление и поток жидкости непрерывны). Решение уравнения с разрывным коэффициентом при старшей производной (3.18) просто выражается через хорошо известные специальные функции - так называемые вырожденные гипергеометрические функции или родственные им функции параболического цилиндра [106]. При О g go решение уравнения (3.18), удовлетворяющее условию (3.20), имеет вид

ф = С ехр i-fm [Da + Da (-гЫЩ. (3.21)

где С -константа. Da -символ функции параболического цилиндра. Из условия (3.17) получаем

С = 1 /2Dа (0) = г [(1 - а)/2]/2 + п.

Здесь Г - символ гамма-функции.

При решение уравнения (3.18), для которого сходится

интеграл (3.16), представляется в виде

ф = f ехр i-m) Da a/V2), (3,22)

где F - константа. Второе линейно-независимое решение убывает на бесконечности, как и интеграл (3.16) для него расхо-

дится. Требуя выполнения условия

-+(1+а)Ф = 0 при 1 = Ь±0,

и используя рекуррентные соотношения для производных функций параболического цилиндра и выражение функций параболического цилиндра через вырожденные гипергеометрические функции [106], получаем:

(о/л/2) = 0, М (-а/2 - 1, 72, о/4е) = 0, (3.23)

где М(а, 6, г)-символ вырожденной гипергеометрической функции.

Эти уравнения должны определять параметр а и величину go в зависимости от е. Далее, условие непрерывности функции Ф при g = go определяет константу F:

F=C[Da (WV2) + (-WV2)] X X ехр 1/8)/8] [D (go/y2)] = [Г ((1 ~ а)/2)/2 + / V] X X [а (со/л/2е) + Da (~У V2e)] X X ехр (1 - 1/е)/8] [D (goV2)] (3.24)

Требование непрерывности производной йФЩ в силу (3.19) удовлетворяется при этом автоматически.

Таким образом, предположив существование автомодельного предельного решения в форме (3.14), мы пришли к классической ситуации нелинейной задачи на собственные значения (нелинейной потому, что координата go точки разрыва коэффициента при старшей производной в уравнении (3.18) заранее неизвестна и должна быть найдена в ходе решения задачи). Действительно, при произвольном а основное уравнение (3.18) нужного по гладкости решения, удовлетворяющего условию (3.17) не имеет. Однако если система (3.23) разрешима, то для а, удовлетворяющего условиям (3.23), решение удовлетворяет всем требованиям.

Для полного исследования решения нам осталось выяснить разрешимость системы трансцендентных уравнений (3.23), определяющей а и go. Решая первое уравнение относительно go/V2,

Аналогично решению такой же начальной задачи для классического уравнения теплопроводности решение рассматриваемой задачи должно убывать на бесконечности быстрее любой степени поэтому интеграл (3.16) для него обязан сходиться.

получаем монотонно возрастающую функцию а (рис. 3.4, кривая 1). Решая второе уравнение относительно go/Vs, получаем монотонно убывающую функцию а (кривая 2). При каждом данном 8 соответствующая зависимость go/V от а получается простым растяжением или сжатием кривой 2 вдоль оси ординат. При 8= 1, т. е. при xi = >c, кривые У и 2 пересекаются при а = О, в соответствии с известными результатами для классического случая; точка их пересечения дает координату точки перегиба функции

ф( 1) = ехр (-2/4), go=V2. При 8=71 точка пересечения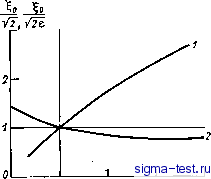

-1 о i 2 ос

Рис. 3.4. Исследование разрешимости системы трансцендентных уравнений (3.23).

1 - зависимость WV2 от а, определенная

из первого уравнения (3.23), 2 - зависимость o/V2e от а, определенная из второго уравнения (3.23).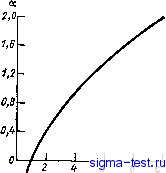

Рис. 3.5. Зависимость собственного значения а от отношения e=Xi/x: при 8<1 а отрицательно, при е>1 а положительно, при 8=1 (классическое линейное уравнение теплопроводности) а=0.

кривых 1 vi 2 единственна. Соответствующая зависимость а от 8 представлена на рис. 3.5. Как видно, при 8>1 величина а положительна, при 8 < 1 - отрицательна. Зависимость а(8), полученная в результате решения нелинейной задачи на собственные значения, хорошо совпала с зависимостью, полученной при численном счете неавтомодельных задач Коши.

Заметим, что кривые 1 и 2 па рис. 3.4 при больших значениях 8 имеют также и другие ветви. Вторая ветвь кривой 1 начинается в точке 0=0, а = 1 и идет, монотонно возрастая, ниже первой ветви. Вторая ветвь кривой 2 двузначна и располагается выше первой ветви этой кривой. Точки, соответствующие пересечениям кривой 1 с этими ветвями, существующие при достаточно больших 8, физически нереальны.

На рис. 3.2 точками показаны значения функции Ф(, 8), полученные решением нелинейной задачи на собственные значения. Как и должно быть, эти точки хорошо ложатся на кривую и{х, t){Kt)+y/A, соответствующую t-oo. Это подтверждает,