слоев. При устойчивой непрерывной стратификации внутренние волны заполняют все пространство, занятое жидкостью, разумеется, если в жидкости имеются источники возмущений. Такие источники в океане и атмосфере имеются всегда (отметим хотя бы приливы, создающие в океане внутренние волны громадной амплитуды и длины), так что внутренние волны представляют собой повсеместно распространенное в океане и атмосфере явление (см., например, [68, 132]). Взаимодействие внутренних волн с турбулентностью является определяющим для турбулентности в стратифицированной жидкости.

12.5. Сильное взаимодействие турбулентности с внутренними волнами. Заглубление турбулизованной области

1. Сильное нелинейное взаимодействие внутренних волн и турбулентности приводит к принципиально новым эффектам. Один из них был продемонстрирован Филлипсом [181], выполнившим замечательный эксперимент, принципиальная схема которого заключается в следующем.

Рис. 12.4. Принципиальная схема эксперимента Филлипса.

; - слой легкой жидкости. 2 - слой тяжелой жидкости, 3 - решетка, возбуждающая турбулентность, 4 - турбулизованная область, 5 - фронт турбулентности.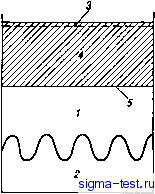

На поверхности раздела двух слоев жидкости разной плотности возбуждаются внутренние волны (рис. 12.4). После установления стационарной системы волн на верхней границе верхнего слоя начинает возбуждаться турбулентность. Турбулизованная область постепенно распространяется вниз от верхней границы верхнего слоя; ее нижняя граница - резкая. Распространение нижней границы турбулизованной области определялось визуализацион-ными методами. Основной эффект заключается в том, что при подходе фронта турбулентности к границе раздела слоев волны сглаживаются и практически исчезают.

Заметим, что на самом деле в опытах Филлипса бак имел форму кругового цилиндра, и турбулентность возбуждалась вра-

щением диска, покрывавшего верхнюю границу верхнего слоя, так что здесь возникало вращательное среднее сдвиговое течение. При теоретическом рассмотрении [12] задача была несколько упрощена: считалось, что слой жидкости горизонтально-однороден, а турбулентность возбуждается без сдвига, например, колебаниями решетки перпендикулярно границе слоя (см. рис. 12.5). Это упрощение, облегчающее теоретическое рассмотрение, ни в коем случае не является принципиальным, не говоря уже о том, что упрощенная схема соответствует вполне реальному опыту [32, 33, 207, 208, 213].

2. Рассмотрим вначале распространение турбулентности, возбуждаемой без образования сдвигового течения на границе г = О бесконечно глубокого горизонтально-однородного слоя жидкости постоянной плотности. Ввиду отсутствия сдвига средней скорости порождение турбулентности средним течением не происходит, так что уравнение баланса турбулентной энергии в области, охваченной турбулентностью, записывается в виде

dtb + <[р7р + (1/2) {и + V + wy + = О (12.43)

(обозначения те же, что и в п. 11.2). Диффузионным потоком турбулентной энергии в уравнении (12.43) пренебречь уже нельзя: именно он определяет основной эффект захвата - расширение турбулентной области. Запишем выражение для диффузионного потока турбулентной энергии в виде

<:[р7р + (1/2) {и + + ш2)] w} = -Кьд,Ь, (12.44)

где Kb - коэффициент переноса турбулентной энергии. Подчеркнем, что запись (12.44) сама по себе не содержит никакой гипотезы: здесь лишь вводится новая характеристика потока Кь-

Примем теперь, как и раньше, для коэффициента Кь и скорости диссипации колмогоровские гипотезы замыкания:

К = 1Ь; Et = cb/l, (12.45)

где с - универсальная в рамках принятой модели постоянная*. Уравнение (12.43) принимает при этих предположениях вид

dtb - dj ф д,Ь + cbll = 0. (12.46)

Уравнение (12.46) близко по типу к уравнениям нелинейной теплопроводности, рассмотренным в главе 2. Начальную турбулентность в поле потока, в соответствии с условиями опыта, можно считать отсутствующей, так что начальную турбулентную энергию примем равной нулю. Приток турбулентной энергии на

Эту постоянную уже нельзя считать определенной из опытов со сдвиговыми течениями. Действительно, приняв Кь равным, а не пропорциональным l/b, мы переопределили /, включив в выражение для него множитель, равный отношению Кь к коэффициенту обмена импульса /С, отличный от единицы.

поверхности слоя q будем вначале считать постоянным. Таким образом, начальное и граничное условия в задаче примут вид

6 (г, 0)0; {l/bдJ)\o=-q, (12.47)

так что турбулентная энергия зависит от величин t, q, г, а масштаб турбулентности, принимаемый постоянным по глубине охваченной турбулентностью области,- от величин t и q. Постоянство масштаба по глубине подсказывается идеей А. А. Таунсенда [205] об определяющей роли больших вихрей в процессе переноса. Анализ размерности дает

b = qff{z/q4); l=aq4, (12.48)

Здесь а - постоянная, которая, так же как и с, в рамках предлагаемой модели не определяется и должна быть найдена из опыта или более детальной теории. Подставляя (12.48) в (12.46) и (12.47), получаем для / обыкновенное дифференциальное уравнение

{dldl) (а Vf dfldl) + I dfldl - cfla = 0, = zlq4 (12.49) и краевые условия

(aVf )=o = -l; f(oo) = 0. (12.50)

Искомое решение, как и в главе 2, отлично от нуля только на конечном промежутке (О, go). Таким образом, в сделанных предположениях турбулентная энергия в момент / отлична от нуля только в области конечной глубины Л, растущей со временем по линейному закону, так что скорость распространения границы турбулентной области получается постоянной:

hiqfH, dhldt = loq\ (12.51)

При этом суммарная турбулентная энергия в турбулизованной области, приходящаяся на единицу площади границы, растет со временем по линейному закону:

\b(z, t)dz = qt\f(dl = o{a)qt, (12.52)

a интегральная скорость диссипации не зависит от времени:

\etdz = \ (I) dl = т (а) cq. (12.53)

Заметим, что, принимая масштаб постоянным по глубине тур-булизованного слоя, мы делаем непринципиальное аппаратное упрощение. Действительно, если считать, что масштаб / зависит также от г, то а во втором соотношении (12.48) окажется функцией g, т. е. a==a(g). Для определения этой функции требуются дополнительные соображения. В широких предположениях отно-