выделившаяся в центре взрыва в начальный момент. Наконец, имеет место очевидное условие отсутствия притока вещества и энергии в центре при / > 0:

у (О, 0 = 0 при />0. (2.20)

Анализ уравнений (2.17) и условий (2.18) -(2.20) показывает, что характеристики движения газа р, р, v зависят от определяющих параметров

ро, г, (2-21)

размерности которых в классе систем единиц измерения MLT суть соответственно:

Г, ML-\ L, 1. (2.22)

Радиус фронта зависит от тех же определяющих параметров (2.21), за исключением г. Таким образом, п = Ъ, k = 3 и, выбирая в качестве определяющих параметров с независимыми размерностями первые три, получаем:

П1 = г(Я ро)-= = Е; П2 = у, (2.23)

откуда и из анализа размерностей следует:

P = 9o{rlt)P{l. у); Р = Ро/?(, Y); v = ir/t)V а, у);

rf = lo (Y) (Et/fioT; D = (Y) (ЕГ%оУ\ (2.24)

Подставляя (2.24) в уравнения (2.17), получаем для функций Р, У, R систему обыкновенных дифференциальных уравнений:

d\nl 5 ) dln

Подставляя (2.24) в граничные условия (2.18), находим:

(-0)=- (2-26)

Здесь, следуя традиции, мы несколько отступили от формального рецепта применения анализа размерностей. Например, для давления следовало бы написать

р=£=ГФ(П Пг).

Выражение для р в (2.24) получается, если обозначить Ф = ЩР, Аналогично и для скорости.

Далее, из (2.24) следует, что полная энергия газа в возмущенной области постоянна во времени, т. е. является интегралом движения:

J!Ljl t

2 (v-

(v-i)pJ

= 4яро U()

(£)

P(l)

(y-1)(1) j

£*d = const. (2.27)

В силу начального условия (2.19) постоянная в правой части (2.27) равна Е, откуда

(y-\)R{l) J

4я

(2.28)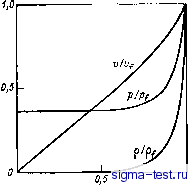

Рис. 2. 2. Распределение давления, плотности и скорости газа за сильной ударной волной в автомодельных переменных р/Р/, PiPf. v/Vf; rjrf.

Решение системы уравнений (2.25) при условиях (2.26) находится, как и в задаче о сильных тепловых волнах, в конечном виде

у = С,У(1 - 1/у (4 1)-;

P=CsR{l--l-V)v[-yV-l)

(2.29)

Здесь

C.=[4 (Y+1)

5(v+l)

J L 7-y J L y-1 J

- 1

13у2-7у+12

1 (3y-1) (2Y-f 1) 2 132-7+12

V4 =

2y+1

(2-y) (3y-1) (2y+1) =

2y+1

2-y

(2.30)

Как нетрудно проверить, решение (2.29) удовлетворяет также условию (2.20). Зависимость go от у определяется подстановкой (2.29) в (2.28) в принципе вполне аналогично тому, как это было сделано в предыдушей задаче. Расчет показывает, например, что 1о= 1,033 при Y= 1,4.

На рис. 2.2 представлено распределение давления, плотности и скорости в виде зависимости универсальных (т. е. одинаковых для всех моментов времени) функций

P/Pf, P/Pf, v/Vf (2.31)

(где р/, р/, Vf - значения величин на фронте ударной волны) от r/rf при Y= 1,4 (воздух).

Изложенное решение было получено Л. И. Седовым [96] и с несколько меньшей полнотой Дж. И. Тейлором [201].

2.3. Автомодельность. Промежуточная асимптотика

Решение задачи о сильном взрыве, как и ранее рассмотренные решения задач о сильной тепловой волне и о мгновенном тепловом источнике, обладает весьма важным свойством автомодельности. Заключается это свойство в том, что пространственные распределения всех характеристик в обеих задачах (температуры в первой задаче, давления, плотности и скорости во второй задаче) в различные моменты времени подобны, т. е. получаются одно из другого преобразованием подобия. Таким образом, если выбрать зависящие от времени масштаб пространственной переменной го(0 й масштаб Uo{t) любой характеристики явления и, то ее распределение в различные моменты представляется в виде Uo{t)X Xf{r/ro(t)). Отсюда следует, что все эти распределения в автомодельных координатах u/uo(t), rlrit) в различные моменты времени представляются единой кривой. Так, в задаче о сильной тепловой волне пространственный масштаб го(0 = [(/с)>] \ масштаб температуры ио{1) = [(£/:)2(х)-з]1/(з+2). g задаче о сильном взрыве го(0 = (Et/Po), масштаб плотности Uo{t) = ро, масштаб давления wo(0 = Ро£ ~Ч масштаб скорости Uo{t) = = {Et~/po)\ Мы уже сталкивались с возможностью такого приведения ранее и говорили о связанных с ним преимуществах.

Как уже отмечалось во. введении, aвтo1vIOдeльныe решения встречаются во многих областях математической физики. Их отыскание привлекало значительное внимание, поскольку в сложных нелинейных задачах получение таких решений, сводящихся к краевым задачам для обыкновенных уравнений, было зачастую единственным средством пробиться через аналитические трудно-

В частности, возможность получения решения в конечном виде связана с указанным Седовым законом сохранения во времени энергии не только внутри всей возмущенной области, но и внутри любой сферы, ограниченной радиусом g=const<o, т. е. г=const(£Vpo)s.

4 Заказ No 208 49