Таким образом, в рассмотрение должны входить дополнительные размерные характеристики: размер головки трещины d, который определяется, вообще говоря, нагрузкой и структурой материала, и характерная величина сил сцепления G,o.

Анализ показывает, что для большого класса практически важных случаев хрупкого и квазихрупкого разрушения справедливы гипотезы [9]: 1) малости размера головки сравнительно с размером трещины / (d/l<l); 2) автономности головки, т. е. одинаковости в состоянии подвижного равновесия головок (и, следовательно, создаваемых ими сил сцепления) для всех трещин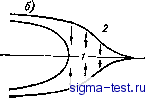

Рис. 9.4. Головка трещины при квазихрупком разрушении: фотография головки трещины в органическом стекле [210] (а) и схема сил сцепления при квазихрупком разрушении (б),

1 - пластическая головка трещины, 2 - упругая область.

В данном материале при данных внешних условиях. Автономность головки трещины объясняется тем, что характерная величина приложенных к телу нагрузок Оо много меньше характерной величины сил сцепления Go (oo/Go<Cl). Поэтому теория хрупкого (и квазихрупкого) разрушения является промежуточно-асимптотической, и оказывается, что существенна не каждая из постоянных d и Go в отдельности: единственной постоянной материала, дополнительной к константам теории упругости является модуль сцеп-ления или трещиностойкость:

(9.42)

Модуль сцепления имеет размерность FL-Ik Он характеризует сопротивление материала распространению трещин и представляет собой независимую характеристику прочностных свойств матери-

Подвижное равновесие отвечает достижению силами сцепления максимума, так что при малейшем увеличении нагрузки трещина начинает распространяться.

ала. Приведем значения модуля сцепления некоторых материалов: органическое стекло - /СЮ кгс/см/% конструкционная сталь -2,5-10 кгс/смЧ дюралюминий -/С 10 кгс/см/.

Модуль сцепления (трещиностойкость) явится одним из определяющих параметров при формулировании законов подобия хрупкого и квазихрупкого разрушения. Появление одного определяющего параметра KGod вместо двух параметров d и Go является типичным проявлением неполной автомодельности.

2. Обратимся к нескольким показательным примерам. Первый из них, рассмотренный в той же фундаментальной работе Гриффитса [133], относится к случаю плоской деформации бесконечного тела с прямолинейной трещиной, растягиваемого одноосным напряжением а, направленным перпендикулярно трещине. Длина / подвижно-равновесной трещины определяется величинами а и /С. Из анализа размерностей получаем

1 = const Ко. (9.43)

Согласно полному решению задачи, const = 4/я Для рассматриваемого вида нагружения катастрофическое развитие трещины, приводящее к полному разрушению тела, начинается при малейшем увеличении нагрузки, после того, как было достигнуто состояние подвижного равновесия. Вообще говоря, как показывает следующий пример, это не обязательно. Рассмотрим в условиях плоской деформации бесконечное тело с прямолинейной трещиной, поддерживаемой двумя противоположными и равными по величине сосредоточенными силами, перпендикулярными трещине и приложенными в центрах противоположных берегов трещины. Размер подвижно-равновесной трещины / зависит от модуля сцепления К и силы 5, приходящейся на единицу толщины тела ([] = FL~), Из анализа размерностей получаем

/ = const (9.44)

Согласно полному решению задачи [9], const = 1. Как видно, при таком нагружении достижение подвижного равновесия не связано с разрушением тела: при дальнейшем увеличении нагрузки трещина растет, но несущая способность тела сохраняется. Если сопротивление распространению трещины, поддерживаемой такими же сосредоточенными силами 5, создается, как это имеет место в горных породах, не силами сцепления, а сжимающим внешним давлением q, то, согласно анализу размерностей,

/ = const 5/. (9.45)

Модуль сцепления, введенный в работе [9], следует отличать от характе-эистики прочности материала Kic, введенной примерно одновременно Ирвином 144] и определяемой по началу катастрофического развития трещины. Катастрофическое развитие трещины требует неустойчивости исходного подвижно-равновесного состояния. Перед началом распространения трещины из неустойчивого состояния автономная головка трещины может не успеть сформироваться. Отсюда большой разброс при определении Kic-

Из полного решения [8] получаем const = 2/я. В этом: случае в отличие от предыдушего, длина трещины растет пропорционально разрывающей силе, а не ее квадрату.

3, В замечательных опытах Бенбоу [111] и Реслера [Гв81 (рис. 9.5) штамп с плоским торцом круговой формы вдавливался, в образец из стекла [188] или плавленого кварца [111]. Под* штампом образуется и с увеличением нагрузки распространяется трещина, имеющая форму усеченного кругового конуса.

Рис. 9.5. Коническая трещина Бенбоу-Реслера, образующаяся при вдавливании штампа [111].

Диаметр D основания конической трещины зависит, очевидно, от действующей нагрузки 5, диаметра индентора d и модуля сцепления К. Из анализа размерностей находим

Д = (5 ()Ф(Щ); Us = S/Kf\ (9.46)

Большие нагрузки отвечают Щ>1, так что если имеет место полная автомодельность по параметру Щ, то должно быть справедливо соотношение

D = const (5 С) const = Ф(оо). (9.47)

Обработка опытов, проведенных со штампами разных диаметров при разных нагрузках [Ш], хорошо подтверждает это соотношение (рис. 9.6).

4. Обратимся к общим законам подобия при хрупком (квазихрупком) разрушении. Можно представить себе параметры нагружения трех типов: размерности напряжения о, натяжения