существенно более слабых свойств ее локальной однородности и локального самоподобия.

Это означает, что для любой точки кривой можно указать малую окрестность А, в которой кривая обладает следующим свойством. Главный член асимптотического представления числа вершин Лп аппроксимирующей ломаной с длиной звена между двумя располагающимися в окрестности А соседними вершинами ломаной с длиной звена ц зависит только от отношения т]/ при T]/g->oo. Таким образом, предполагается, что с точностью до малых величин число вершин Лп ломаной с длиной звена g внутри одного звена ломаной с длиной звена ц не зависит от места этого последнего звена и от величины и т] при фиксированном отношении T]/g>l:

Лл = /(ЛД). (8-15)

Возьмем теперь новую ломаную с еще меньшей длиной звена <. В силу локальной однородности и самоподобия с точностью до малых величин число ее звеньев внутри одного находящегося в окрестности А звена длиной ц равно, с одной стороны, /(л/) а с другой стороны - произведению числа /(л/Ю звеньев длиной внутри одного звена длиной ц на число /(/) звеньев длиной g внутри одного звена длиной Приравнивая, получаем функциональное уравнение для функции f:

f{x)f{y/x) = f{yl (8.16)

совпадающее с уравнением (1.5) (см. главу 1). Здесь х = ц/1у у = ц/1. Гладкое решение этого уравнения имеет вид f(x) = х. Величина D может быть различной в разных точках кривой. Переходя от числа звеньев к длине ломаной, получаем, что для длин аппроксимирующих ломаных в окрестности каждой точки непрерывной кривой, обладающей свойствами локальной однородности и локального самоподобия, справедливо степенное асимптотическое соотношение

A = riV- + (8.17)

где точки означают величины, малые сравнительно с первым членом (сюда же попадает вклад от крайних звеньев, которые могут оказаться нецелыми). Если повсюду Z) > 1, это означает, что рассматриваемая кривая является фрактальной.

Еще раз отметим, что множество кривых, обладающих свойством локальной однородности и локального самоподобия, неизмеримо богаче множества кривых типа триады Коха, обладающих весьма специальными свойствами полной однородности и самоподобия.

Фрактали проявляют свойства неполной автомодельности по параметру. Покажем это на том же примере фрактальных кривых. Действительно, длина ломаной, аппроксимирующей непрерывную кривую между двумя ее точками, отстоящими на расстояние т],

зависит от двух размерных параметров: ц и длины звена ломаной . Из анализа размерностей получаем

1 = цФШ, (8.18)

Для гладкой (или кусочно-гладкой) кривой при т. е.

при функция Ф стремится к конечному пределу Ф(оо).

По определению, величина

Lo = 0(cx))n (8.19)

представляет собой длину отрезка гладкой кривой между двумя ее точками, отстоящими на расстояние ц. Так, например, если рассматриваемая кривая - окружность, опирающаяся на отрезок длиной ц как на диаметр, то Ф(оо) = я/2. Таким образом, для гладких кривых имеет место полная автомодельность по параметру ц/1 при

Для фрактальных кривых конечного предела функции Ф{г]/1) при л/-оо не существует; этот предел равен бесконечности. Однако из соотношения (8.17) следует, что при цЦ-оо функция Ф{ц/1) имеет степенное асимптотическое представление:

Ф(n/E)-(rl/a)- (8.20)

т. е. имеет место неполная автомодельность по параметру при Y]/g~oo. Ясно, что размерность Хаусдорфа D зависит от геометрических свойств кривой и соображениями анализа размерностей определена быть не может.

Заметим в заключение, что переходя от геометрических образов к представляемым ими физическим объектам, мы можем просто отождествить фрактальность и неполную автомодельность по параметру.

Глава 9

ПОЛНАЯ И НЕПОЛНАЯ АВТОМОДЕЛЬНОСТЬ УПРУГОСТИ

И РАЗРУШЕНИЯ

9.1, Задача о равновесии упругого клина под действием пары сил, приложенной в его вершине

Рассмотрение линейных задач теории упругости поучительно: для них можно аналитически явно проследить выход на автомодельную асимптотику решений невырожденных задач и переход при некотором критическом значении параметра от автомодельностей первого рода к автомодельностям второго рода. Для нелинейных задач этого так просто сделать не удается.

Мы разберем вначале отдельные задачи теории упругости при плоской деформации, когда компоненты упругих полей - тензоров напряжений, деформаций, вектора смещения и т. д. - одинаковы во всех плоскостях, перпендикулярных некоторому направлению. Уравнения упругого равновесия при плоской деформации имеют, как известно, следующий вид [см., например, 76, 64]:

дгОгг + деОгв/г + (Огг - Огв)/г = 0; деОее/г + дгОгв + 2огв/г = 0. (9.1

Здесь г, е - полярные координаты в плоскости деформации, Огг, Ore, (Уев - соответствующие компоненты тензора напряжений (для дальнейшего нам понадобятся именно полярные координаты).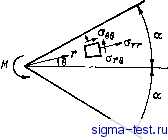

Рис. 9.1. Клин с углом раствора 2а под действием пары сил с моментом Af, приложенной в его вершине.

Уравнения (9.1) тождественно удовлетворяются введением функции напряжений Эри Ч:

(9.2)

Закон Гука связывает линейными дифференциальными соотношениями три компоненты тензора напряжений с двумя компонентами вектора смещений Ur и we, откуда вытекает, что компоненты тензора напряжений удовлетворяют некоторому условию интегрируемости: соотноилению совместности. Если подставить в это соотношение выражения (9.2) компонентов тензора напряжений через функцию напряжений, то для последней получается бигармоническое уравнение

-2 -.2 12

4=0.

(9.3)

Начнем с показательной задачи, впервые рассмотренной в работах Карозерса [118] и Инглиса [140]. Возьмем бесконечный клин с углом раствора 2а и в вершине клина приложим сосредоточенную пару с моментом М (рис. 9.1). Функция напряжений Ч, определяющая распределение напряжений, зависит от четырех параметров: М, г, 0 и а, размерности которых в классе FLT соответственно равны f, L, 1,1. (Размерность момента пары сил в плоской задаче теории упругости совпадает с размерностью силы, поскольку в задаче речь идет на самом деле о паре, прихо-