

 |
 |
|
|
Навигация
Популярное
|
Публикации «Сигма-Тест» Промежуточная асимптотика (развивающееся направление) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 [ 33 ] 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82  концентрации велики (порядка l/e), можно считать скорость реакции равной нулю. Промежуточные, переходные области должны быть узкими, относительной шириной не более е, так как изменение температуры и концентрации в них ограничено, а градиенты имеют порядок l/e. Отсюда следует, что вся область, занятая газом (рис. 6.1), распадается на: 1) области, занятые не сгоревшим холодным газом, где реакция еще не идет, так как газ не успел разогреться; 2) области, занятые горячими продуктами сгорания, где реакция уже не идет, так как все горючее вещество там сгорело, и узкие переходные области, где идет реакция горения и происходят процессы переноса- диффузии и теплопроводности. Если перейти к пределу при е О, т. е. в первом внешнем приближении, переходные области становятся поверхностями разрыва, на которых претерпевает разрыв скорость, плотность, температура и концентрация, но не давление. Скорость распространения по Рис. 6.1. Область движения разбивается на область, занятую свежей горючей смесью (/), область, занятую продуктами сгорания (2), и узкую переходную область, в которой протекает химическая реакция, процессы диффузии и теплопроводности. газу поверхностей разрыва - пламен (нормальная скорость пламени)- из уравнений движения и условий баланса массы, импульса и энергии на поверхностях разрыва не определяется. Можно считать эту величину физико-химической константой, задаваемой независимо, например, определяемой из эксперимента. При этом получается замкнутая система соотношений так называемой газодинамической теории горения [63]. Для аналитического определения нормальной скорости распространения пламени следует обратиться к внутреннему асимптотическому представлению решения и рассмотреть явления в переходной зоне, взяв за характерный масштаб Li = /Dx, а за характерное время т. Выберем направление нормали к средней линии переходной зоны (см. рис. 6.1) за направление координаты х, отсчитываемой от средней линии, и перейдем к безразмерной переменной g = х/л/Dx, отвечающей масштабу Li. Из-за узости переходной зоны только производные по I имеют порядок единицы. Производные по остальным пространственным переменным, имеющие, если брать в качестве характерного внешний масштаб L, порядок единицы, в новом масштабе пренебрежимо малы. Оставляя в уравнениях баланса горючего вещества и энергии только главные члены, запишем эти уравнения в виде рдп + qV din = di()din- Ф {п, и), ро ди + poV ди = dl {kjO) diu -f QФ (n, и). (6.24) Здесь V =VxlDlx\ t;: -компонента скорости смеси вдоль оси х\ Q = t/x - быстрое время, т. е. безразмерное время, отнесенное к масштабу т. Далее, в том же приближении уравнение сохранения массы запишется в виде d + dpV = 0. (6.25) Будем искать решение уравнений (6.24) -(6.25) типа бегущей волны: n = N(0\ u = U{0; V = V{0; t, = l-Xi) + c, (6.26) где с - произвольная постоянная, X - неизвестная и подлежащая определению скорость распространения бегущей волны. Подставляя (6.26) в (6.24) и (6.25) и имея в виду, что p==p(f/(C)) = /?a), получаем для определения неизвестных функций Л, U, V систему обыкновенных дифференциальных уравнений: .,R + RV = R-OiN, U), -Ш+ЯУо=± + ОФ(Ы, U), (6.27) Интегрируя последнее уравнение, получаем: -XR + RV = const (6.28) Распределения температуры, концентрации и скорости в переходной зоне должны удовлетворять очевидным краевым условиям: с одной стороны переходной зоны, там, где она граничит со свежей горючей смесью, горение еще не началось, газ покоится и его температура задана; с другой стороны переходной области горючее сгорело полностью. В соответствии со стандартной асимптотической процедурой, ввиду малости внутреннего масштаба Li по сравнению с внешним L, первое граничное условие следует ставить при S = оо, второе - при g = -оо: N{oo)=U и{оо) = щ; iV(-co) = 0; V{co) = 0. (6.29) Подставляя условия (6.29) в (6.28), приводим это соотношение к виду X{po-R) + RV = 0, (6.30) Здесь ро-плотность свежей горючей смеси. Подставляя (6.30) в первые два уравнения (6.27), находим: Из физической химии известно, что если горючее вещество и продукты сгорания имеют близкий молекулярный вес, можно считать величину kIpoD равной единице. При этом предположении, умножая первое уравнение (6.31) на Q/a и складывая оба уравнения, находим, что система (6.31) имеет интеграл (Q/a) N{i) + U (С) = const, (6.32) называемый в теории горения законом подобия полей концентрации и температуры Льюиса-Эльбе. Из условий (6.29) находим const = ui + Q/o, откуда и из интеграла (6.32) получаем и{--о) = щ + Q/o=U2. (6.33) 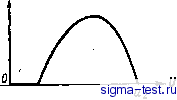 Рис. 6.2. Функция W(U) обращается в нуль на некотором интервале вблизи и=щ. Щ U+k Используя закон подобия (6.32), можно расщепить систему (6.31) и свести ее к одному уравнению для температуры где i 4(f/) = (Q/Poa)0[l-a(f/~t/0/Q, f/]p(f/)/Po. (6.35) По предположению Ф{п, и)=0 при + Следова- тельно, поскольку величина p{U) положительна и ограничена, функция W{U) тождественно равна нулю на отрезке Uiu г/1-ЬД, обращается в нуль при U = U2 и положительна при Ui + A<u<U2 (рис, 6.2). Полагая р = (p{U)/po)dU/dt, и считая и независимой переменной, приводим уравнение (6.34) к виду р dpjdU + Xp + W{U) = 0. (6.36) Из условия (6.29) следует, что интересующее нас решение уравнения (6.36) удовлетворяет очевидному условию обращения в нуль потоков тепла на границах переходной зоны: dUidl = Q при &=dzco, (6.37) Как отмечалось выше, это условие обеспечивает устойчивость исходного состояния. Действительно, положим в уравнениях (6.24) дп и ди тождественно равными нулю, т. е. л и м будут зависеть только от времени. Тогда, если принятое условие выполняется, при малом изменении температуры не начинается реакция. Как будет показано ниже, это условие не является необходимым.
|
|
© 2010 www.sigma-test.ru Санкт-Петербург: +7 (812) 265-34-48, +7 (812) 567-94-10
Разработка и поддержка сайта: +7(495)795-01-39 после гудка 148651, sigma-test.ru(my_love_dog)r01-service.ru Копирование текстовой и графической информации разрешено при наличии ссылки. |