u = dh/dt и его избыточная температура во-будут функциями некоторого безразмерного медленного времени Т:

ии(Т); 00 = 00(Г). (12.35)

Пренебрежем горизонтальной неоднородностью и будем считать, что движения, определяющие механизмы турбулентности и тепло- и массообмена в верхнем термоклине, стационарны, однородны и мелкомасштабны. Тогда в сделанных предположениях для осредненной избыточной температуры 0 (г, /) получается уравнение теплопроводности

dQ=:yidlz&. (12.36)

где t - время, а х - эффективный вертикальный коэффициент температуропроводности, который мы принимаем постоянным. Заметим, что в последующем рассмотрении было бы нетрудно учесть переменность этого коэффициента и, в частности, его зависимость от температуры и/или ее градиента. Дальнейший анализ покажет, однако, что в таком усложнении нет необходимости.

Распределение осредненной избыточной температуры удовлетворяет граничным условиям

в (А, О = 00 (Г); 0(оо, 0 = 0. (12.37)

Перейдем к подвижной координате - /г, отсчитываемой от

верхней границы термоклина. Тогда уравнение (12.36) и условия (12.37) запишутся (ср. аналогичное рассуждение в п. 6.5) в виде

0(0, t) = %{T)\ 0(со, 0 = 0. (12.38)

В рассматриваемой задаче характерный масштаб времени т = = yi/uy имеет, как будет показано, порядок нескольких суток. Поскольку 0 -осредненная избыточная температура, кратковременные процессы на нее влияния не оказывают, и следует считать время t большим т. При больших t решение задачи (12.38) асимптотически становится стационарным, так что производная (30 в уравнении (12.38) исчезает. Получающееся уравнение легко интегрируется, и при условиях (12.38) находим

0 = 0oexp(-i/x). (12.39)

Удобно ввести универсальную переменную - относительную температуру 6 = (0о - 0)/0о. При этом решение (12.39) записывается в виде

е= 1 ехр (-аЕ/х), (12.40)

т. е. распределение относительной температуры оказывается автомодельным. Автомодельность распределения относительной температуры в верхнем термоклине была эмпирически обнаружена С. А. Китайгородским, Ю. 3. Миропольским и Б. Н. Филюшкиным

[53, 69] при обработке натурных опытных данных. П. Линден [161] предпринял полезную попытку обработать на основе гипотезы автомодельности данные своих опытов по определению профилей солености на лабораторной модели верхнего термоклина. В работе О. В. Решетовой и Д. В. Чаликова [90] путем обработок натурных опытных данных была установлена аналогичная автомодельность для поля солености в верхнем термоклине. Б. В.Харьков [102] критически проанализировал методику обработки натурных опытных данных и также подтвердил автомодельность распределения относительной температуры в верхнем термоклине океана. Однако во всех этих работах автомодельность не связывалась с тем или иным физическим механизмом, В предыдущих главах мы уже неоднократно убеждались, что автомодельность не бывает случайной: она всегда свидетельствует об определенной стабилизации процесса. Выход температурного поля в верхнем термоклине на стационарную бегущую волну - еще один показательный пример, это иллюстрирующий. Модель бегущей волны применительно к верхнему термоклину была предложена и апробирована опытными данными - лабораторными и натурными - в работе [14]; одновременно и независимо близкую модель предложил Дж. Тернер [209]. Следует отметить, что стационарное решение уравнения теплопроводности с подвижным тепловым источником (12.39) было впервые указано Г. Герцем еще в прошлом веке и с тех пор многократно использовалось в различных областях математической физики. В частности, оно играет фундаментальную роль в теории горения, описывая распределения температуры в области, где химическая реакция еще не идет (см. главу 6). Модель бегущей тепловой волны неоднократно использовалась и в океанологии: по образному выражению У. Манка [169], применившего близкую модель в другой физической ситуации, она восходит к океанологической древности. Интегрируя (12.40), получаем:

k/a=j (1-0)1, (12.41)

так что соотношение (12.40) переписывается в универсальном виде

In 1/(1 - в) = / S (1 е) 4 = (12.42)

Таким образом, если предлагаемая модель верна, то в координатах In 1/(1-6), опытные точки должны лечь на биссектрису первого координатного угла. В работе [36] С. С. Ефимов и В. М. Царенко провели обработку в этих координатах многочисленных натурных данных, хорошо подтвердивших модель бегущей волны для верхнего термоклина. На рис. 12.3 представлены результаты Ефимова по обработке осредненного за октябрь 1968-

1972 гг. профиля температуры на станции погоды Эхо (34°0с. ш, и 48°0 3. д.), любезно предоставленные Б. Н. Филюшкиным. Как видно, эти данные подтверждают принятую модель тепловой волны для верхнего термоклина и постоянство эффективного вертикального коэффициента температуропроводности.* Приведенные данные позволяют получить некоторые показательные оценки. Для натурных измерений на станции Эхо величина х/г, определенная, согласно формуле (12.41), составляет примерно 2-10 см. Оценивая среднюю скорость опускания верхней границы термоклина, получаем: иЮ.., 10 см/с. Отсюда и из предыдущей оценки находим нЮ *... 1 смс. Это значение является проме-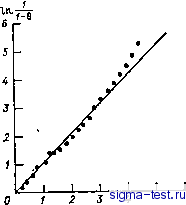

Рис. 12.3. Результаты обработки натурных экспериментов подтверждают модель бегущей волны для верхнего термоклина.

жуточным между порядком молекулярного коэффициента температуропроводности воды, равным примерно 10~ см/с, и порядком коэффициента турбулентной температуропроводности в верхнем однородном слое, составляющим 10 см/с Полученная оценка для эффективного вертикального коэффициента температуропроводности совпадает с оценкой У, Манка [169] для промежуточной по глубине области Тихого океана и согласуется с глобальной оценкой Г. Стоммела [196]. Аналогичное промежуточное значение коэффициента обмена получается и по данным лабораторных опытов. Это дает основание предположить (Филлипс [182]), что обмен в верхнем термоклине определяется перемежающейся турбулентностью, связанной с разрушением внутренних волн.

Внутренние волны представляют собой специфическое для среды с устойчивой стратификацией явление. В случаях, когда стратификация дискретна т. е. в многослойной жидкости, плотность которой убывает снизу вверх от слоя к слою, энергия внутренних волн сосредоточена в основном вблизи границ раздела

Систематические отклонения в верхней части графика, отвечающей нижней области термоклина, объясняются способом обработки, при котором в этой области теряется точность.