Как и для всякого автомодельного решения второго рода, константа go остается в построенном асимптотическом решении неопределенной, поскольку закон сохранения турбулентной энергии принимает неинтегрируемую форму.

8. Следующее замечание также относится к притоку энергии на границе турбулизованной области. Представляется естественным, что плавно увеличивая со временем частоту колебаний решетки, т. е. суммарную подачу энергии в оба слоя, можно при определенной скорости роста частоты обеспечить постоянный приток турбулентной энергии внутрь турбулизованной области, а следовательно, и линейный закон ее заглубления. Это было проверено в работе [33]. В новой серии опытов частота колебаний решетки

Рис. 12.11. Зависимость толщины турбулизованного слоя от времени в универсальных координатах при переменной частоте колебаний перфорированной пластины и Y=0,80 [33].

Сплошная линия отвечает h-i-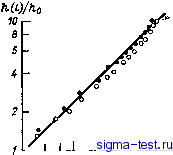

40 60 80100 200 mtot/to

плавно возрастала по степенному закону со (t/to), где /о, у - постоянные. На рис. 12.11, взятом из [33], показано, что при у = = 0,80 в случае решетки в виде перфорированной пластины закон заглубления турбулизованной области действительно близок к линейному.

Далее, при достаточно длительном колебании решетки в однородной жидкости нижняя граница турбулизованной области достигает дна бассейна, после чего через некоторое время в бассейне устанавливается стационарный режим турбулентности. Очевидно, что в стационарном режиме турбулентная энергия b зависит от частоты со и амплитуды а колебаний решетки, а также от глубины Z точки наблюдения под решеткой и глубины бассейна Я. Анализ размерности дает

Ь = а(х?Фь{г1а, Н/а).

(12.68)

Ясно, что в основной части бассейна, вне непосредственной близости решетки параметр г/а>1, поэтому можно ожидать, что распределение турбулентной энергии описывается предельными соотношениями. Если бы по параметру z/a была полная автомодельность, то распределение турбулентной энергии по глубине было бы равномерным: b = aWO{oo, Н/а). Опыты Томсона и Тернера

[204] показали, что это не так, и имеет место соотношение неполной автомодельности по параметру г/а:

b==Caii{alzY, (12.69)

причем показатель степени п и константа С существенно зависят от формы решетки.

9. В предыдущем рассмотрении предполагалось, что сдвиг.отсутствует. Однако автомодельные асимптотики рассматриваемого типа должны иметь место и при возбуждении турбулентности со сдвигом.

Действительно, уравнения баланса импульса и энергии в нестационарном однородном по горизонтали в среднем турбулентном потоке с поперечным сдвигом имеют при тех же предположениях вид

dtU - dj л/Ъд,и = О, (12.70)

dtb - dEbl фдф + ybll -l(d,uf=0, (12.71)

где u{z, /)-средняя скорость, - постоянное отношение коэффициента обмена турбулентной энергии к коэффициенту обмена импульса, а остальные обозначения прежние. Как нетрудно видеть, эти уравнения допускают автомодельные решения вида

u = Ai-gi\ b = AH-f{l); l = zlAt-\ l = aAt-. (12.72)

Соответствующая система обыкновенных уравнений для функций g и f легко выписывается. Аналогично предыдущему, нелинейность уравнения турбулентной энергии такова, что при отсутствии начальных турбулентных возмущений, т. е. при начальном условии 6 (г, 0)=0, область, где решение g, / отлично от нуля, конечна и соответствует О g go, а следовательно, конечна и глубина турбулизованной области в каждый момент: h = oAt~. При g = go имеют место очевидные условия

Wfdf/dl\===0; WTdV/dl\=0, (12.73)

вытекающие из обращения в нуль на нижней границе турбулизованной области потока импульса и потока турбулентной энергии.

10. Специфика распространения турбулентности в стратифицированной жидкости заключается в передаче части энергии на границе турбулизованной области внутренним волнам, возбуждаемым в нетурбулизованной стратифицированной жидкости, лежащей под турбулизованной областью. Автомодельность распространения турбулентности при этом сохраняется только в том случае, когда энергия, передаваемая внутренним волнам, составляет постоянную часть т (0<т<1) энергии, поступающей в турбулизованную область от решетки. Все сказанное выше при этом

остается справедливым за исключением первого условия (12.73), которое заменяется условием

{агьл/Тс1Ш1\=1. = --т. (12.74)

Разумеется, показатель степени в законе расширения турбулизованной области при этом будет зависящим и от величины т.

Предположение о постоянстве доли энергии, передаваемой турбулизованной областью внутренним волнам, делалось рядом авторов (см. [161, 208]). Если бы оно не выполнялось, наблюдавшаяся автомодельность заглубления турбулизованной области не имела бы места.

Заметим, наконец, что нами принималось предположение о постоянстве масштаба турбулентности по глубине турбулизованной области. В автомодельном представлении это предположение свело дело к единственной константе а, которая в рамках предложенной схемы не определялась. Можно воспользоваться известным полуэмпирическим подходом Лаундера [137] или каким-либо другим аналогичным подходом, основанным на введении нового дифференциального уравнения, позволяющего определить масштаб. При этом величина a(g) станет определяемой переменной величиной, зависящей от основной автомодельной переменной. К сожалению, такого рода подходы всегда приводят к мало достоверным гипотезам замыкания и к необходимости введения новых параметров, предполагаемое постоянство которых всегда нуждается в трудном обосновании.

12.6. Разрушение внутренних волн и растекание пятен перемешанной жидкости в устойчиво стратифицированной жидкости

Взаимодействие внутренних волн и турбулентности в жидкости с сильно устойчивой стратификацией не сводится только к перераспределению волновой энергии турбулентностью, которое было рассмотрено в предыдущем параграфе. Турбулентность в устойчиво стратифицированной жидкости имеет своеобразную пространственную структуру. Наблюдения, в частности в верхнем термоклине океана, показывают, что она сосредоточена в блинообразных слоях - пятнах турбулентности, простирающихся в горизонтальном направлении на расстояния, значительно превышающие их толщину [70, 73, 101]. Эти блинообразные пятна оказываются резко ограниченными и сравнительно долго живущими. Даже после затухания турбулентности жидкость в них долго остается перемешанной. Поэтому возникновение и развитие пятен перемешанной жидкости в устойчиво стратифицированной среде представляет значительный интерес, в частности (см. ни,же), в связи с тонкой структурой и микроструктурой океана.

Возникновение пятен перемешанной жидкости связано с разрушением внутренних волн, которое может обусловливаться раз-