математиками конца девятнадцатого - начала двадцатого века, в частности, в связи с построением примеров непрерывных нигде не дифференцируемых функций. Большинству физиков они казались, а некоторым кажутся и поныне, математическими уродцами, не имеющими приложений в реальных задачах естествознания и техники. В действительности это не так.

Возрождение интереса к подобным объектам и осознание их важной роли в приложениях обязано серии работ, и в особенности примечательной монографии-эссе Б. Мандельброта [164]. Ман-дельброт ввел термин фракталь и общее понятие фракталей. Он показал, что вопреки ожиданиям это понятие, охватившее многие известные частные примеры, оказалось плодотворным в таких разнообразных и важных приложениях, как физика полимеров и геоморфология, теория броуновского движения, теория турбулентности и астрофизика, а также многих других. Именно фрактали, как оказалось, представляют собой адекватный образ многих интересных природных объектов. В монографии [164] изложены также с единой точки зрения относящиеся к этим вопросам предшествующие работы других авторов.

В этой главе мы расскажем о фракталях Мандельброта, опираясь на простейший пример фрактальных кривых, разберем свойства однородности и самоподобия, которые делают непрерывную кривую фрактальной и покажем, что основная идея фракталей тесно связана с неполной автомодельностью по параметру.

Начнем с одного показательного результата. Известным английским физиком Л. Ф. Ричардсоном была предпринята попытка [187, 164] измерить длину морского побережья острова Британия. Ричардсон выбрал следующий естественный для обычных гладких кривых способ определения этой длины. Он приблизил линию побережья на детальной карте Британии замкнутой ломаной линией, составленной из отрезков постоянной длины г], все вершины которой располагались на побережье. Длина Lti этой ломаной принималась за приближенное значение длины побережья, соответствующее данному значению ц. Предполагалось, что при уменьшении Г] соответствующие значения длин аппроксимирующих ломаных L, будут стремиться к определенному конечному пределу, который и следует принять за длину морского побережья.

Естественно, что так и получилось, когда этот способ был применен к изображенной на той же карте окружности (рис. 8.1, кривая а). Однако в отличие от гладкой кривой - окружности, линия морского побережья оказалась настолько изрезанной вплоть до самых малых изображенных на карте масштабов, что с уменьшением длины звена аппроксимирующей ломаной ц величина Ьц к конечному пределу не стремилась. Напротив, величина Ьц с уменьшением т) неограниченно возрастала, причем во всем имевшемся диапазоне значений т) это возрастание происходило по степенному закону (рис. 8.1, кривая б):

= W (8.1)

где А,:>0 и D> 1 - некоторые постоянные. Для приближенной длины отдельных участков того же побережья между некоторыми его точками также получались соотношения вида (8.1) с теми же £), но другими, меньшими К. Когда такое же определение было по* вторено для побережья Австралии (рис. 8.1, кривая в), степенной закон сохранился, но уже обе постоянные к и D оказались другими. Как видно, постоянная D безразмерна, постоянная же к имеет причудливую размерность длины в дробной степени D.

Формальный переход к пределу при т]->0 в соотношении (8.1) дает малосодержательный результат: определяемая по предложен-

/,{? 1,5 2,0 2,5 3,0 Lg 71

Рис. 8.1. Зависимость длины Ly ломаной, аппроксимирующей морское

побережье, от длины ц ее звена: а - окружность, б - Западное побережье Британии, в - побережье Австралии.

ному способу длина морского побережья и, добавим, длина любого его отрезка бесконечны. В то же время из (8.1) следует, что отдельные куски побережья можно сравнивать по некоторой мере их протяженности, хотя и не по длине. Действительно, приблизим оба куска побережья ломаными с одной и той же длиной звена т]. В обоих случаях получаются соотношения вида (8.1):

(8.2)

Как видно, отношение (2)Д(1) длины звена лома-

ной т] не зависит. Таким образом, протяженность отдельных участков побережья можно сравнивать, но не по их длинам, а по соответствующим им коэффициентам к. Таким образом, сам подход к определению протяженности морского побережья теми же средствами, что и для гладких кривых, оказался неприменимым.

Адекватным представлением для линии морского побережья является не гладкая кривая типа окружности или эллипса, дл-я которой предел длины аппроксимирующей ломаной Ьц при стремлении к нулю длины ее звена т] конечен, а кривая-фракталь, для

которой это не так. Представление о кривых-фракталях (или фрактальных кривых) дает так называемая триада Коха [154, 164] (рис. 8.2). Для ее построения возьмем исходный равносторонний треугольник (рис. 8.2 а) и подвергнем на первом шаге каждую из его сторон элементарной операции -peLSennu ее на три равные части и заменим среднюю часть двумя другими сторонами построенного на ее базе равностороннего треугольника (рис. 8.2 6). На следующем шаге той же элементарной операции подвергается каждая из сторон получившегося на первом шаге двенадцатиугольника и т. д. В результате на п-м шаге получается ломаная линия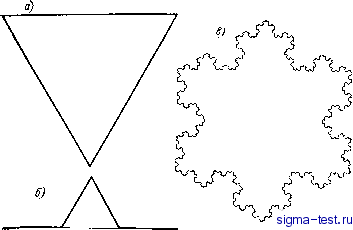

Рис. 8.2. Триада Коха.

а - исходный треугольник, б - элементарная операция, в - аппроксимирующая ломаная линия при большом п.

типа границы многоугольника, изображенного на рис. 8.2 в. Продолжая до бесконечности, получимнепрерывную кривую, нигде не имеющую касательной,-триаду Коха.

Суммарная длина и длина ц звена получившейся на п-м шаге ломаной линии определяются следующим образом:

Z, = 3Z(4/3)- л = /3 (8.3)

где L - длина стороны исходного равностороннего треугольника. При п-оо длина звена ц стремится к нулю, а длина всей ломаной Ьц - к бесконечности. Второе из соотношений (8.3) дает п = = Ig (L/r])/lg 3, так что первое соотношение (8.3) приводится к виду

,alg(/n) 3()a (8.4)

Z=3Z.10°

где а = (Ig 4 - Ig 3) /Ig 3 = 0,2618... - трансцендентное Положим

1 = 1; D=l+a = lg4/Ig3=l,2618 . ..,

число.

(8.5)