степенным (рис. 3.1). Точнее, спустя некоторый промежуток времени после начала счета выполняется соотношение

где А и а -некоторые константы. Численные расчеты показали, что при изменении начальных условий менялась только константа Л, константа же а оставалась неизменной: оказалось, что она зависит только от 8 = Ki/k.

Величина Uo{t) = А/{Kt)- может служить естественным масштабом для переменной и(х, t). Возьмем в качестве линейного

масштаба /кt и построим график зависимости величины и{х, t)/Uo{t)=u{x, Щк1)-1А

от xlyit для разных моментов времени X (рис. 3.2). Оказывается, что с увеличением времени эти кривые быстро стремятся к совпадению, так что их зависимость от времени исчезает.

Таким образом, численный эксперимент показал, что решение задачи Коши для уравнения (3.1) быстро выходит на автомодельную промежуточную асимптотику

и{х, t) = {A{yitf\ф{xJty е), (3.10)

где показатель а зависит только от е = xi/x - отношения коэффициентов в уравнении (3.1), тогда как А зависит и от начальных условий.

3.5. Автомодельное предельное решение

Разберемся теперь, как могла появиться у решения задачи Коши асимптотика (3.10), хотя и тоже автомодельная, но отличающаяся от предсказанной анализом размерности формы (3.5).

Как уже было отмечено, начальное условие (3.4), которое привело нас к решению в форме (3.5), имеет предельный характер, описывается обобщенной функцией и в машинный счет непосредственно заложено быть не может. На самом деле в ходе численного эксперимента на машине считалось решение, удовлетворяющее начальным условиям (рис. 3.3), описываемым обычными функциями вида

и{х, 0) = {Q/l)uo{x/t), (3.11)

где / - некоторый пространственный масштаб, характеризующий размер области, из которой в начальный момент была удалена жидкость:

оо со

Q= J и{х, 0)dx; \ Uo{OdZ=l.

- оо -со

Здесь wo(0 - безразмерная, четная, финитная (обращающаяся в тождественный нуль для достаточно больших значений абсолютной величины своего безразмерного аргумента) функция. Для таких начальных условий уже можно быть уверенным, что решение задачи Коши существует, единственно и обладает непрерывными производными по X до второго порядка и непрерывной производной по t\ это следует из доказанных общих теорем. Однако в этой задаче появился новый размерный определяющий параметр /, и ее решение уже не будет автомодельным. В самом деле, стандарт-

и(х,0)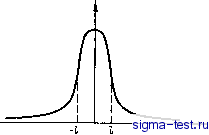

Рис. 3.3. Начальное условие неавтомодельной задачи Коши, решение ко-X торой заведомо существует.

пая процедура, основанная на анализе размерностей и продемонстрированная выше на нескольких задачах, дает здесь

(3.12)

Рассмотренное выше автомодельное точное частное решение типа мгновенного источника для случая xi = % отвечало сингулярному начальному условию, получающемуся из (3.11) при /=0. Но это решение типа мгновенного источника шире, чем просто точное частное решение отдельной задачи. Действительно, соотношение (3.12), справедливое и при е = 1, показывает, что цО не только при /->0, но и при too и любом / = const > 0. Выбирая соответственно х, можно этот предельный переход осуществлять так, чтобы Izxl/nt оставалось постоянным; в пределе получается известное автомодельное решение, указанное выше. Таким образом, как уже отмечалось, автомодельное решение задачи с сингулярными начальными данными при к\ = к представляет собой асимптотику широкого класса решений начальной задачи при больших временах. Решение задачи с сингулярными начальными данными (3.4) при к\Ф%, в согласии со сказанным, не существует. Это означает, что при кхФп не существует конечного, отличного от нуля предела функции F{, г], е) при т]-0. Тем не менее, как показали численные расчеты, автомодельная асимптотика решения (3.12) все же существует, хотя и не в форме (3.5), а в форме (3.10). Наличие у решения (3.12) автомодельной асимп-

тотики (ЗЛО) при t->oo подсказывает, что при для функ-

ции F{1, Г], г) справедливо асимптотическое представление

F{1, Я е) = Г1 /(, е) + 0(г1 ).

Именно поэтому при t->oo асимптотическая форма решения рассматриваемой задачи уже не представляется в виде (3.5), но имеет форму

u = [Qr/{ntf + - ]f{l,e), (3.13)

где функция /(g, г) конечна и отлична от нуля.

Заметим теперь, что стремление ц к нулю при конечном g мо\ жет осуществляться также путем предельного перехода при 1->0 и неизменных х и t. Как хорошо известно, при таком предельном переходе в классическом случае xi = х, 8 = 1 снова получается решение типа мгновенного источника. Выражение (3.13) показывает, что если выполнять этот предельный переход, оставляя Q неизменным, то при афО предел решения будет равен нулю или бесконечности в зависимости от того, положительно а или отрицательно. Для того чтобы при аф О получить с помощью предельного перехода /-0 и неизменных л: и то самое предельное выражение решения задачи, которое получается при конечном / и /->оо, нужно переходить к пределу при /->0, устремляя одновременно Q к бесконечности или нулю в зависимости от знака а и притом так, чтобы оставалось конечным произведение Ql. Получающееся при таком предельном переходе автомодельное предельное решение имеет уже не форму (3.5), но представляется в виде

и = [Л/(хО°1Ф(Е, 8); A = plimQr; Хо{1)=1ол/- (ЗЛ4)

Здесь р - безразмерная постоянная, которая зависит от нормировки функции Ф(, 8), а параметр а - след исчезнувших при предельном переходе параметров Q и /. Параметр а можно определить, выполняя, например, при помощи численного счета, предельный переход от решения неавтомодельной задачи к автомодельной асимптотике. При прямом построении автомодельного предельного решения подстановкой (3.14) в основное уравнение и начальные условия параметр а неизвестен и подлежит определению. Таким образом, определение параметра а явно фигурирует в формулировке задачи, составляя часть определения автомодельного предельного решения.

Заметим теперь, что для решения (3.14) момент

\ \х\и{х, t)dx (3.15)

Символом 0(х) обозначается, как обычно, величина порядка х\ символом о{х) - величина, малая по сравнению с х.