что приводит к дальнейшим упрощениям РЯ-линеаризованного уравнения Рейнольдса, которое в этом случае можно заменить уравнением в вариациях с последующим применением к нему преобразования Лапласа.

ГЛАВА IV

СТАЦИОНАРНЫЕ РЕШЕНИЯ

ЛИНЕАРИЗОВАННОЙ ЗАДАЧИ ГАЗОВОЙ СМАЗКИ ДЛЯ НЕКОТОРЫХ ТИПОВ ОПОР

В этой главе дается решение основных краевых задач газовой смазки для стационарных режимов ротора. Эти режимы возможны лишь при постоянных нагрузках и отсутствии дисбалансов и погрешностей форм несущих поверхностей ротора.

Решение краевых задач статики и определение основных статических характеристик подшипников производится на базе основного уравнения Рейнольдса методом, указанным в конце предыду-дущей главы. Как будет видно из дальнейшего, этот метод дает возможность рассмотреть с единой точки зрения подшипники с произвольным профилем на несущей поверхности, в том числе подшипники со спиральными или шевронными канавками. Существенно, что основные результаты для шевронных, или спиральных, подшипников могут быть получены методо1\4 РЯ-линеаризации лишь во втором приближении. В работе Уилдмена и др. [46, т. 90, № 4; т. 91, № 1 ] показано, что РЯ-линеаризованное решение уравнения Рейнольдса в первом приближении не обнаруживает эффекта поперечного нагнетания *, создаваемого спиральными канавками. Уточнение, которое получается в результате вычисления второго приближения, весьма существенно и для подшипников с простым периодическим профилем, частным случаем которых является цилиндрический подшипник с гладкой втулкой или втулкой, профилированной системой осевых канавок.

В дальнейшем упомянутый метод решения краевых задач газовой смазки мы будем называть обобщенным методом РЯ-ли-неаризации, подразумевая под этим метод РЯ-линеаризации Османа [54, т. 83, № 2; т. 85, № 4], дополненный вторым приближением.

* Употребляемые автором термины продольный и поперечный эффекты нагнетания условны. В стационарном режиме работы газодинамической опоры, в том числе подшипника со спиральными канавками, единственным источником несущей способности является эффект смазочного клина, обусловленный переменностью толщины смазочного слоя в направлении скольжения. Подшипник со спиральными канавками может иметь более высокую несущую способность за счет дополнительного смазочного клина, создаваемого вдоль оси канавки, вследствие наличия составляющей скорости скольжения по этой оси и изменения толщины смазочного слоя на стыке канавки с непрофилированной зоной (зоной утечки).

15. Решение стационарной задачи для гладкого цилиндрического подшипника

Впервые решение краевой задачи статики для цилиндрического подшипника с гладкой втулкой было получено С. А. Шейнбергом на основании численного уравнения Рейнольдса. Несколько позже та же задача была решена численным интегрированием уравнения Рейнольдса с помощью ЭВМ. В результате этих работ в настоящее время в теории газовой смазки имеются достаточно подробные таблицы для расчета основных статических характеристик цилиндрического подшипника. Несмотря на это, были предприняты исследования уравнения Рейнольдса с целью получения аналитического решения краевой задачи статики. Дело в том, что при исследовании динамики ротора статические характеристики опор приходится использовать в качестве исходных данных, а использование этих данных в виде таблиц крайне затруднительно. Поэтому, например, в работе Г. А. Поспелова [44] при исследовании устойчивости ротора в цилиндрических подшипниках цифровые данные из работы [57] интерполируются с помощью тригонометрических полиномов. В связи с этим в данном параграфе приводится аналитическое решение упомянутой краевой задачи обобщенным методом РЯ-линеаризации.

Рассмотрим цилиндрический шип в цилиндрическом подшипнике, вращающийся вокруг своей оси с постоянной угловой скоростью Q. Предположим, что ось шипа смещена относительно оси подшипника и остается параллельной последней. Положение

шипа относительно подшипника определим вектором е (рис. 21). Предположим, что положение центра шипа О соответствует равновесию внешних нагрузок и реакций смазочного слоя. Тогда вектор смещения е можно считать постоянным. Для определения реакций смазочного слоя необходимо решить основное уравнение распре деления давления (3.20) при соответствующих граничных уело виях: Pj=±i = 1; Рф = Р1ф+2я (так как решается стати ческая задача, то нестационарный член д {НР)1дх отбрасывается) Преобразованное уравнение (3.20) с помощью подстановки (3.41, к виду (3.42), дает уравнение и граничные условия краевой задачи статики для цилиндрического подшипника в виде:

(¥фЯ- ¥Яф)]ф + о§ {riH-WHi)l - t,T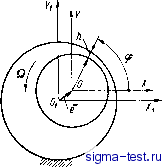

Рис. 21

0; (4.1)

iF/£=±i = Я/£=±1; ¥/ф = ¥/ф+2я,

(4.2)

00 =

. Хо -

обозначения остальных величин, входящих в уравнение (4.1).

даны в гл. III.

Для рассматриваемого здесь случая . с целью упрощения выкладок положим = еу = 0; Ео = е/б. Отбрасывая в (3.21) последний член, который для гладкого подшипника равен нулю, получим для функции зазора следующее выражение:

Я = 1бо cos ф. , (4.3)

Применим к решению (4.1), (4.2) обобщенный метод РЯ-линеаризации (см. гл. III). Согласно (3.48) уравнение (4.1) в 1-м приближении будет иметь вид

(ЧОфф + аЬ - Хо СОф = Яфф + aoHk, i S К 1 (4.4) Делая подстановку

W, = H + Y, (4.5)

приведем краевую задачу 1-го приближения к однородным граничным условиям:

+ ooYi - ХоГф = хоЯф-, (4.6)

К£=±, = 0; }ф = Гф+2л = 0. (4.7)

С целью сокращения выкладок решение (4.6), (4.7) будем проводить в комплексной форме. Для этого рассмотрим следующую краевую

Хфф + 0§Хц-хоХф = Хо;; (4.8)

Х£=±, = 0; Хф=Х:ф+2 , (4.9) где Ж - комплексная функция зазора,

=1 -бое-ф. (4.10) Нетрудно заметить, что, решив (4.8), (4.9), найдем решение и для

У=Ке\Ж\. (4.11) Решение краевой задачи (4.8), (4.9) ищем в виде

= ео/(9е-ф. (4.12)

Подставляя (4.12) в (4.8) и учитывая условия (4.9), придем к уравнению для функции / (Р

аГ -(1 -ixo)/ = tXo, /(±1) = 0. (4.13)

Решение этого уравнения может быть записано в таком виде:

т[-] (4-И)

где -Lyi-ixo . 90

Заметим, что уравнение (4.13) экЁИВалентно йИстеме двух вещественных уравнений с двумя неизвестными функциями, а его решение (4.14) представляет собой комплекснозначную функцию вещественная и мнимая части которой суть решения эквивалентной системы дифференциальных уравнений с вещественными коэффициентами. Таким образом, мы получили решение РЯ-линеаризо-ванного уравнения (4.4) в квадратурах.

Действительно,-подставляя / ($) из (4.14) в (4.12) и отделяя вещественную часть согласно (4.11), получим из (4.5) искомое решение

,¥1 = Я+ eoRe -

1 - fXo

- pj. (4.15)

Решение (4.15) соответствует решению Османа, которое отличается от него только по форме [53, т. 83, № 2; т. 85, № 41. Сравнение этого решения с решениями других авторов проводилось Константинеску [25]. Это сравнение показало, что решение 1-го приближения по методу РЯ-линеаризации вполне удовлетворительно, а при введении поправочного коэффициента дает хорошую количественную оценку.

Для уточнения решения (4.15) подставим ¥i из (4.15) в уравнение аддитивной поправки (3.55). Подстановка дает

2я 2Я

[чг,(г,я-¥,ЯЕ)]£аф = -1} (¥!Я)каф.(4.1б)

При преобразованиях здесь учитывалось, что все функции периодичны по ф, а Я = 0. Учитывая далее, что аддитивная поправка Д () должна обращаться в нуль при = ±1, и интегрируя (4.16) по I, получим

{) - \\Нй + [\ + \г) (4.17)

1 - Хо

Хо 1 + Хо

1 - ео cos ф + ео (/е * + /*е<Р) X (1 - eocos ф)ф.

ch9o J

ch 9o -

; ?o = - V1 + ixo

Вычисляя интегралы, получим выражение

A(0 = eg[Re{/(0l--If(01]. (4.18)

Решение 2-го приближения запишется так:

= 1 + А (Q - Я + бо Re {f (О е-ф1 -f

+ e.g[Re{f(Q)-4/(Qp]. (4.19)

При больших числах сжимаемости Хо можно получить оценку точности этого решения из сравнения с точным предельным решением

3 2

(4.20)

Переходя к пределу при Хо+ в (4.19) и учитывая, что Иш / (Q = 1, будем иметь

¥2со = lim ¥2= 1 +4-ео. (4.21)

Учитывая, что

1 + -- eg = 1 + -f о - +

получим оценку погрешности в предельном случае I 42 -

в частности, при е < 0,5

<

а при ео < 0,8

3211 + l,5eg

< 0,015, J <0,082.

(4.22)

Как будет видно из дальнейшего, обобщенный метод РЯ-линеаризации достаточно чувствителен и дает возможность исследовать эффекты второго порядка, которые оказывают определяющее влияние на работу подшипников со спиральными канавками.

16. Статическая реакция цилиндрического подшипника с гладкой втулкой

На базе полученного решения (4.19) можно вычислить все статические характеристики подшипника: несущую способность, жесткость, момент сопротивления и т. д. Здесь мы ограничимся вычислением главного вектора сил давления, действующих на шип со стороны смазочной пленки. Если пренебречь тангенциаль-92

ными силами tpeHHH по сравнению с нормальными силами давления, то последние и будут определять статическую реакцию подшипника. Главный вектор сил давления вычисляется по следующей формуле:

F, = F-i-iF = -paR P (4-23)

Интегрирование в (4.23) проводится по всей поверхности шипа S : О Ф = 2я; I. Учитывая, что

Р-1=.

и принимая во внимание решение (4.19), получим

PaRL

О О 2л

еФЙф = - ео

f* f йф + ео J Re 1/1 J -

0 2Я

2л 2Я

(4.24)

Введем обозначения: 1

= J[l

dl; =A + iB; * = A~iB.

Учитывая выражения (4.14), будем иметь: 1

f с Хо (Хо - ) 7 .

f* иг - Ь (Хо + )

(4.25)

Подставляя (4.25) в (4.24) и вычисляя прочие интегралы (см. приложение 1), после простых преобразовании получим

Л 2яво Х5 + Хо5 (J 3 2.

PaRL

(4.26) 93