Система координат OiXiYZi жестко связана со статором гироскопа, а система координат OXYZ имеет начало О в центре масс ротора и ее орты параллельны ортам опорной системы OX,Y,Z,.

Смещение центра масс О ротора относительно статора опре-

делим вектором е, а ориентацию оси фигуры - проекциями

->

орта S° на оси координатной системы OXYZ. Заметим, что ориентацию оси4игуры можно определить либо углами Эйлера аир,

либо двумя проекциями вектора С на оси ОХ и 0Y.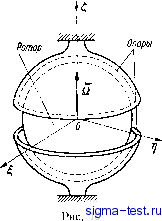

Второй способ позволяет записать уравнения движения гироскопа в комплексной форме, удобной для решения задач устойчивости газодинамических подшипников, поэтому ему оказано предпочтение.

Обозначим через Q угловую скорость собственного вращения ротора вокруг оси фигуры, тогда вектор мгновенной угловой скорости ротора можно представить в виде

со = Q -I- Ml,

(2.1)

где coi - экваториальная составляющая угловой скорости. Учитывая, что

(2.2>

Составим выражение для вектора момента количества движения ротора

(2.3)

где / - экваториальный; 1 - осевой моменты инерции, теореме об изменении момента количества движения имеем

dk dt

ИЛИ, учитывая (2.1), (2.2) и (2.3),

t° X

dt I

(2.4)

(2.5)

Обозначим через X, Y и Z проекции 1,° на оси OX, OY, OZ, тогда

1° = X°X + Y°Y + ZOZ. (2.6)

Проектируя уравнение (2.5) на оси OXYZ и учитывая при этом равенство (2.6), получим:

I (YZ-ZY) + kX + KX = + ,;

I {ZX - XZ) + KY + KY =S?y+ у,; (2.7)

где К = /о - кинетический момент; Sy, Sz - проекции главного момента всех сил реакций смазочного слоя, действующих на ротор; Ув. zb - проекции главного момента внешних

сил.

Уравнения (2.7) эквивалентны уравнениям движения симметричного гироскопа [2] и отличаются от последних отсутствием в коэффициентах тригонометрических функций. Уравнения (2.7) обладают замечательным свойством симметрии, которым воспользуемся для приведения их к комплексной форме.

Будем определять угловое положение оси ротора с помощью комплексной величины

V =X+iY {i=V~). (2.8)

Умножая первое уравнение (2.7) на i и вычитая почленно из второго, получим систему двух уравнений:

IZU - IZU ~ i{KU + Ки) = - i {Sx -Ь is у) - i {ЗБх. + iSy.Y.

/С = Z + ZB,

(2.9)

где

Z = V\-X-~Y =1/1 -I (/f.

В системе уравнений (2.9) комплексное уравнение представляет первые два нелинейных уравнения из (2.7).

Поступательные движения ротора относительно кожуха можно также описать дифференциальным уравнением в комплексной

форме. Действительно, по теореме о движении центра масс будем иметь в проекциях на оси ОХ, 0Y, 0Z:

Mex = Fx + Fx; Mey = fy+fy,; Mez = Fz + Fz, (2.10) где М - масса ротора; Fx, Fy, Fz - проекции главного вектора сил реакции подшипника; Рхъ> Fy, Fzb - проекции возмущающих сил.

Если представить е = вх + iey; F = Fx + iFy, F = Fxb + + fyg, TO уравнения (2.10) будут иметь следующий вид:

+ 1 (2.11)

Mez = Fz + Fz,.\

Члены уравнений с индексом в обозначают внешние возмущающие силы и моменты.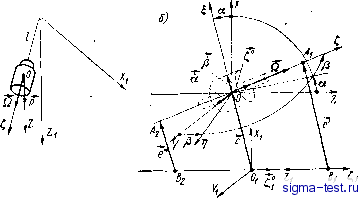

Рис. 12

Таким образом дифференциальные уравнения движения ротора одноопорной машины разбиваются на две подсистемы (2.9)- (2.11), описывающие соответственно сферическое и поступательное движения. В правых частях этих уравнений стоят силы и моменты, которые зависят от координат и их производных. Силы и моменты могут быть записаны в комплексной форме и в общем случае являются некоторыми функциями комплексных переменных и, е ш вещественных переменных е, й, t.

На основании уравнений (2.9)-(2.11) можно компактно изложить основные законы движения симметричного гироскопа в случаях Эйлера и Лагранжа [2]. Например, в случае тяжелого гироскопа Лагранжа, полагая вх = еу= = О, = О, из (2.9) получим:

IZU - JZU-iKU = ~PlU, /С = const. (2.12)

На рис. Г2 показана ориентация относительно выбранной системы координат симметричного гироскопа: а - силы тяжести Р;

б - опор двухопорного гироскопа (машины). В уравнении (2.1) предполагается, что сила тяжести Р направлена по оси 0Z, центр тяжести О ротора смещен на величину / от центра опоры 0.

Для нахождения всех возможных случаев прецессии гироскопа достаточно представить искомое решение уравнения (2.12) в виде:

(i = aexp(tQO- (2.13)

Подстановка (2.13) в (2.12) приводит к простому алгебраическому уравнению относительно постоянной а:

maY\-d +KQa = ~Pla. (2.14)

Из решения этого уравнения могут быть выведены все возможные стационарные режимы движения гироскопа. Анализ устойчивости этих режимов при периодических возмущениях можно провести методами нелинейной теории колебаний [35; 1; 48].

Уравнения (2.9), (2.11) могут быть использованы для изучения динамики сферического гироскопа. Последний обычно работает в режиме свободного гироскопа. Для того чтобы сферический гироскоп с газодинамическим подвесом был свободным, его кожух устанавливается на стабилизированную платформу, которая управляется с помощью следящей системы так, чтобы ось фигуры , ротора была все время совмещена с общей осью подвеса и статора. При таком совмещении осей тормозящий момент сил вязкого трения уравновешивается крутящим моментом электрического привода, в силу чего кинетический момент гироскопа К остается постоянным. Все это верно в условиях отсутствия гравитационного

поля и инерционных перегрузок, когда смещение центра масс

-> ->

ротора равно нулю (в = 0).

При смещении центра масс ротора под влиянием внешних сил тяжести или сил инерции момент тангенциальных сил вязкого трения полностью не уравновешивается и появляется экваториальная составляющая этого момента, которая порождает вредную прецессию. Для газодинамических подшипников моменты Sx, Sy, Sz и силы Fx, Fy, Fz в уравнениях (2.9)-(2.11) являются функциями смещений е, еу, и времени t.

Структура этих функций изучается в теории газовой смазки. Здесь же ограничимся выводом нелинейной системы дифференциальных уравнений (2.9), (2.11) в комплексной форме. Эти уравнения справедливы для любой машины с неподвижным статором, ротор которой имеет симметричный эллипсоид инерции.

5. Уравнения движения двухопорной машины с учетом угловых перемещений статора

Рассмотрим маш1ну с ротором, вращающимся в двух сферических подшипниках, геометрические центры которых не совпадают. Предположим, что оба тела - статор и ротор машины-

имеют симметричные эллипсоиды инерции, причем статор может совершать лишь сферическое движение относительно некоторой точки Oi, а ротор может совершать как сферическое, так и поступательное движения. Отнесем систему статор-ротор к системе координат OiXiYiZi, движущейся поступательно. Положение центра масс ротора О в этой системе координат опреде-

лим вектором е = 00, а ориентацию -единичными векторами t°

и Qi, направленными соответственно по осям симметрии эллипсоидов инерции ротора и статора (рис. 12, б).

Расстояние между центрами цапф ротора Ai и равно 21, положение центров цапф относительно Опор иВа определяется векторами смещений е и е .

Предположим, что вал ротора оканчивается двумя сферическими цапфами, расположенными на одинаковом расстоянии от центра масс ротора О, а оси симметрии эллипсоидов инерции ротора и статора совпадают соответственно с геометрическими осями симметрии цапф и подшипников.

Для того чтобы получить уравнения движения машины, введем систему координат OXYZ с началом в центре масс ротора и осями, параллельными осям опорной системы координат OiXiYZi.

Единичные векторы ° и определяющие мгновенную ориентацию осей фигур ротора и статора, представим в проекциях на соответствующие оси координат OXYZ и OiXiYZi.

(2.15)

1,0= X°X-\-Y°Y + Z°Z; Z = Yl - X~Y; Й = да,+К?К,+Z?Z,; Zi=Vl~X!~Y! Q , vO v-o vO лэ to

одесь-л , r ., z. , Л], Y\, Zi - орты соответствующих осей координат; X, Y, Z; Xu Fi, Zi - проекции векторов t°, на оси координатной системы OXYZ, движущейся поступательно вместе с центром масс ротора О.

Рассматривая сферические движения ротора и статора отдельно, каждое из которых происходит под действием своей системы сил, можно написать уравнения, описывающие эти движения [см. уравнение (2.9)1:

jzu~izu~i (ки + ик)==~i+ k = Sz + Sz.\

hZ,U\~hZ,V,-i{k,U,+lj,K,) =-i(, + ); .

кг = Szl + ziB-

(2.16)

Здесь и = X + iY; Ui = X + iY - комплексные координаты, определяющие угловое положение оси фигуры ротора и 44

статора; S = Sx + iSy - проекция на плоскость OXY вектора результатирующего момента всех сил, действующих на ротор;

S?xi +iSyi - Щоектя на плоскость OiXiFi вектора результатирующего момента, действующего на статор; Sz и S?zi - осевые составляющие соответствующих моментов; К = /о и /( = /oii - кинетические моменты ротора и статора соответственно; /, Ii - эквивалентные моменты инерции; Iq и - полярные моменты инерции; Q и Qi - угловые скорости собственного вращения ротора и статора.

Левые части уравнений (2.16) содержат в качестве неизвестных две комплексные переменные U я Ui я две вещественные - /( и Ki- Моменты, стоящие в правых частях, являются функциями переменных U, Ui, е, е.

Таким образом, взаимодействие между ротором и статором устанавливается по правым частям уравнений (2.16).

Векторы моментов S я Si, действующих на ротор и статор соответственно, можно представить в виде:

S - /С X (Г - F ) + S-ic -Ь S, + Snp + 1 = - /1 X [F - f ) - ic -.

np

(2.17)

Здесь F и f - главные векторы реакций смазочного слоя под-

шинников, продолженных к цапфам и А; Sic и Sc - моменты тангенциальных сил / сопротивления, действующих на -

цапфы; - момент привода с учетом момента сопротивления

аэродинамических сил, действующих вне смазочной пленки; S

и Sis - возмущающие моменты, которые включают моменты сил инерции переносного движения основания и гравитационных сил.

Поступательное движение ротора будет совершаться под действием сил инерции и гравитационных сил, а уравнения поступательного движения запишутся согласно теореме о движении центра масс следующим образом:

Мё F +F + F\

Mez =Fz + Fz + Fz.

(2.18)

где e = ex + tey; F= FxiFy, F =F x+ iFV, F Fx + iFy. Силы F, F , Fz, F z определяются из решения уравнения Рейнольдса и представляют собой функции угловых и линейных перемещений цапф в подшипниках (см. гл. III).

Уравнения (2.16), (2.18) представляют собой замкнутую систему дифференциальных уравнений движения машины, содержащую в качестве неизвестных три комплексные U, Ui, е к три вещественные К, Ki, переменные, которые в свою очередь являются функциями времени t. Уравнения (2.16), (2.18) углового