четырьмя переменными: давлением р и тремй Составля1рщими вектора скорости газа у, Уц, уф, которые связаны между собой следующими уравнениями Рейнольдса [25; 311:

1 др йУф .

R sin е йф

R дЬ

= 0;

(3.2) (3.3) (3.4)

sin е

1 d(pvQ)

(3.5)

Здесь t - время; R - радиус шипа; ц - динамический коэффициент вязкости. Эти уравнения являются частным следствием общих уравнений ламинарного движения вязкого газа (уравнений Навье-Стокса), в которых согласно допущениям п. 9 отброшены инерционные члены, а также все члены порядка О {hJR), где ho - характерная толщина смазочного слоя; в реальных газовых подшипниках ho/R 10 *. Границы области интегрирования системы уравнений -(3.2)-(3.5) определяются границами несущих поверхностей. В случае, когда несущая поверхность подшипника имеет вид сферического пояса, область интегрирования уравнений будет лежать между двумя параллелями, т. е. 6i + 8xC6C < 02 + 82, где 61 и 62 - углы, определяющие границы сферического пояса при е = 0; и - малые вариации, обусловленные

вектором смещения е, которыми следует пренебречь каквеличи-нами порядка О {ho/R).

Уравнения (3.2) и (3.3) проинтегрируем дважды по переменной г с учетом того, что согласно (3.4) давление не меняется поперек смазочного слоя а коэффициент р принимается постоянным (см. п.9). При интегрировании используем характерные для сплошной среды условия прилипания газа к несущим поверхностям шипа и подшипника. В результате получим следующие выражения продольных составляющих скорости газа через давление [25; 31 ]:

1 др

ут =

2цН sin 6 1

у0 =

(Эф др

2iiR dQ

iy-hy)V (1-г)

(3.6)

где h ~ h {(р, Э, /) - зазор между несущими поверхностями; у = г - R - радиальная координата сферической системы, отсчитываемая от поверхности шипа; ф, Vq-проекции вектора

линейной скорости поверхности шипа. Этот вектор можно определить по формуле Эйлера, известной из курса теоретической механики:

de dt

+ (ох/?.

Вектор угловой скорости шипа ю относительно системы координат OXYZ можно представить в виде

(3.8)

где Q - угловая скорость собственного вращения ротора; coj -

экваториальная составляющая вектора со, обусловленная угловыми колебаниями оси вращения. Направление этой оси опре-

->

деляется единичным вектором С , который совпадает с осью Z при отсутствии колебаний (рис. 14).

В сферических подшипниках составляющая со обычно весьма

мала по сравнению с со и ее влияние на распределение давления в смазочном слое незначительно. Поэтому положим сояО, что приводит к следующим приближенным выражениям для иско-

мых проекцией вектора V:

(3.9)

Основное уравнение теории газовой смазки в сферических координатах получается из уравнения сплошности (3.5) путем почленного интегрирования по координате г в пределах от г = R т г = R + h с учетом выражений (3.6) и граничных условий для поперечной скорости у, которые следуют из того, что скорость газа..на твердой поверхности равна скорости самой поверхности. После соответствующих выкладок получим

2R sin е д(р V 6ni? sin еу

2R sin е 66

B{hpV,

hp dp eilR d&

= 0.

(ЗЛО)

Введем следующие обозначения: б - минимальный зазор между несущими поверхностями сферического шипа и подшипника при центральном положении шипа; Е - половина максимальной глубины мй роканавок; ра - давление окружающей атмосферы; Р = р/ра - относительное давление в смазочном слое; Я =

= д - относительный зазор. Используя (3.9) и умножая

все члены уравнения (3.10) на надлежащий размерный множитель, приведем основное уравнение газовой смазки, описывающее распределение давления в смазочном слое и обьгчно называемое

уравнением Рейнольдса, к безразмерному виду

(язя--) + зте1(зтеязя) =

=xsine+sineli5).

Эф - (3.11)

Здесь X = t - безразмерное время; % = -j--e

определяющий критерий подобия газодинамических подшипников, который будем называть параметром сжимаемости, следуя принятой терминологии.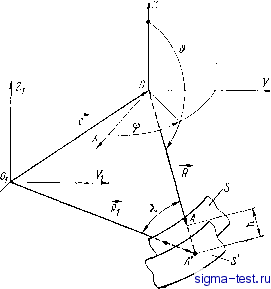

Рис. 15

Полученное нелинейное дифференциальное уравнение второго порядка содержит три независимые переменные 9, ф, т.

Если уравнение (3.11) рассматривается изолированно от уравнений динамики опоры, то относительный зазор Н считается заданной функцией координат и времени. Чтобы определить вид

этой функции, обратимся к рис. 15. Через R обозначен радиус-вектор произвольной точки А на несущей поверхности шипа-5 в системе координат OXYZ, связанной с центром шипа. Несущая

поверхность подшипника 5 пересекается с направлением Я в точке А {АА = h), радиус-вектор которой в системе координат OiXYZi, связанной с центром подшипника, обозначен

через Ri. При наличии искусственного профиля, нанесенного на 72

неподвижную поверхность S, из рис. 15 непосредственно Следует векторное равенство

где hi - глубина искусственного профиля в точке А. Почленное

скалярное умножение на вектор R/R приводит это равенство к виду

л /? + б + Л, , (е. R) 1 -1----- COSA--5а-.

Представим скалярное произведение (е, R) через проекции векторов на оси системы координат OXYZ, тогда с учетом того, что

cosX= 1 -0(),.

из предыдущего равенства получается следующее приближенное выражение для толщины смазочного слоя:

h = /ii - excos ф5ш9 - зШф sin9 -ezCosQ,

->

где вх, ву, ez - проекции вектора смещения е на соответствующие оси. Наконец, разделив все члены этого выражения на 8 -\- Е, где Е = /iin,ax/2, получим искомую безразмерную функцию зазора

Н = 1 - Ех cos ф sin 9 - 8у sin ф sin 9 -

- 8zCos9 + Ti (9, ф). (3.12)

Здесь 8 = е/{8 + £) - относительный эксцентриситет шипа, который может зависеть от времени; ц = Е/ф + Е) - безразмерный параметр искусственного профиля; и (9, ф) - знакопеременная функция (-1 и eg +1), определяющая форму профиля.

Таким образом, структура основного уравнения (3.11) полностью определена>, Оно является ключевым при решении задач газовой смазки. Проинтегрировав его при соответствующих граничных условиях, которые будут рассмотрены в п. 11, можно затем вычислить динамические реакции подшипника, и если это необходимо, с помощью соотношений (3.6) найти распределение скорости в смазочном слое, что, в свою очередь, позволяет рассчитать трение в подшипнике [31].

11. Основные типы граничных условий к уравнению Рейнольдса и способы постановки краевых задач для сферического подшипника

Наиболее типичными граничными условиями к уравнению Рейнольдса (3.11), описывающему распределение давления в смазочном слое сферического подшипника, или к подобным ур.авне-

ниям для газовых подшипников иной геометрии (см. п. 12) являются: -а

а) условие непрерывности решения вблизи внешнего контура смазочного слоя Г, которое имеет вид

Р/г=1, (3.13)

если за масштаб давлений принято давление окружающей среды;

б) условие периодичности решения по одной из координат; например, для случая, когда функция распределения толщины смазочного слоя (Н) в уравнении (3.11) является периодической по координате ф с периодом 2л;, оно имеет вид

Р(Ф,0, О = Р(ф + 2я,0,О. (3.14)

Заметим, что непрерывность решения обеспечивается во всей области интегрирования, включая контур Г, если функция Н внутри области непрерывна или имеет конечные разрывы (то или другое, очевидно, всегда выполняется), а физические параметры подшипника - число сжимаемости х и число Струхала 5 в уравнении Рейнольдса* - остаются ограниченными. В специальных случаях оо и 5 - оо уравнение имеет бесконечно малый параметр при старших производных, порядок его понижается, что приводит к нарушению непрерывности давлений вблизи контура Г или, по крайней мере, некоторых его участков, а также линий скачкообразного изменения толщины смазочного слоя (Диприма [46, т. 90, № 3], Константинеску [25] и др.).

В п. 9 уже указывалось, что если на смазываемой поверхности подшипника имеются ступеньки или изломы-линии, нарушающие непрерывность или гладкость функции распределения толщины смазочного слоя Я, то их следует, строго говоря, рассматривать как особые линии в области интегрирования уравнения Рейнольдса, поскольку на них не выполняются некоторые основные допущения теории смазки; вблизи этих линий более правильно было бы применять общие уравнения Навье-Стокса. Поэтому наиболее корректным представляется такой подход к решению уравнения Рейнольдса, когда область интегрирования делится на ряд подобластей, внутри каждой из которых функция Я является непрерывной и гладкой, и решения, полученные для каждой подобласти, сращиваются на вышеупомянутых особых линиях. Если отвлечься от специальных случаев х-о°и5-оо, тов качестве одного из условий сращивания решений на линии нарушения непрерывности или гладкости функции Я следует принять условие непрерывности решения

Р~ = Р\ (3.15)

* Последний член уравнения (3.11) должен содержать множитель 2xS, однако в данном случае этот множитель оказывается равным единице за счет соответствующего формального выбора масштаба времени.

где индексы минус и плюс соответствуют точкам, расположенным непосредственно перед и за линией сращивания.

Совокупйостьусловий(3.13)-(3.15) недостаточна для однозначного определения искомого решения уравнения Рейнольдса в каждой из рассматриваемых подобластей. Дополнительные условия можно установить, исходя из того, что уравнение Рейнольдса (3.11) физически является частным следствием закона сохранения массы. Оно связывает изменение массы газа в элементарном объеме hR sin ЭЭф с массовым расходом через поверхность, ограничивающую этот объем. На вышеупомянутых линиях сращивания, где нарушаются основные допущения, использованные при выводе уравнения Рейнольдса, оно несправедливо, и здесь закон сохранения массы выражается в форме следующего условия баланса массовых расходов:

пГ = т*; т = ру Я,

где р - плотность газа; у -г- осредненная по толщине смазочного слоя величина составляющей скорости газа, направленной вдоль поверхности слоя по нормали к линии сращивания. При постоянной температуре в смазочном слое (см. п. 9) из (3.15) следует, что р- = р , и тогда условие баланса массовых расходов можно заменить условием баланса объемных расходов:

(3.16)

Если же линия сращивания представляет собой излом (Я = Н*), то получим простое условие непрерывности осредненной скорости потока смазки v = vt- Условие (3.16) применимо к газодинамическим опорам любой геометрии. Для сферического подшипника в случаях, когда линия сращивания направлена по меридиану или расположена параллельно плоскости экватора, соответственно будем иметь, используя выражения (3.6):

(3.17)

Только что описанный способ постановки краевых задач газовой смазки, связанный с- введением дополнительных условий сращивания (3.15), (3.16) на линиях, где терпят разрыв коэффициенты уравнения Рейнольдса или их производные по координа- , там, оказывается неудобным для практического использования при большом числе линий разрыва в области интегрирования, а также при их несовпадении с координатными линиями (вдоль которых обычно направлены границы области интегрирования). В подобных случаях, характерных для подшипников, профилированных спиральными канавками, более целесообразной может быть аппрокси-