мещений гироскопа: .

(6.65)

При построении амплитудно-фазовых частотных характеристик подсистемы угловых колебаний необходимо учитывать, что передаточная функция эквивалентного разомкнутого контура Go(s, i) имеет полюсы Sj, 2 = О и Sg = i/x, которые расположены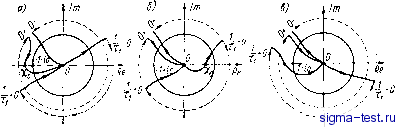

Рис. 35

на мнимой оси комплексной плоскости s. Поэтому при определении условий устойчивости рекомендуется пользоваться теоремой Руше*, из которой критерий Михайлова-Найквиста вытекает как следствие.

Условия устойчивости (6.65) относятся к подсистеме угловых колебаний и их выполнение не гарантирует устойчивости всей системы, к условиям устойчивости (6.б5) необходимо добавить еще условие (5.39).

Полученные выше условия (6.65) могут быть уточнены количественно путем вычисления вихревой жесткости на основе результатов предыдущих параграфов.

Кроме того, можно получить уточнение отдельных фрагментов частотных характеристик путем учета коэффициента утечки и т. д.

32. Вычисление моментов сил трения

Выше при исследовании поступательных колебаний ротора тангенциальными силами трения мы пренебрегали и учитывали только главный вектор нормальных сил гидродинамического давления. Правильность такого упрощения при исследовании устойчивости подтверждается теорией и практикой [25; 58].

* Привалов И. И. Введение в теорию функций комплексного переменного. (Учебник для вузов). Изд. 2-е. М. Наука , 1967. 444 с.

При исследовании точности приборов пренебрежение соста-вляюй;ей главного вектора сил трения может оказаться недопустимым. Кроме того, для расчета механических характеристик двигателя необходимо знать главный момент сил трения, приложенных к ротору.

Расчет главного момента сил трения в простых радиальных подшипниках можно производить по известным формулам [25; 58].

Здесь мы остановимся на вычислении главного момента сил трения в случае радиального подшипника с шевронными канавками.

Рассмотрим равновесный режим вращения ротора. Главные момент и вектор тангенциальных сил вязкого трения, действующих на один шип, можно найти по следующим формулам:

= iR jj Tie* d(fdz.

(6.66)

(6.67)

Здесь Tj - напряжение сил трения на поверхности шипа; Fj = = Ffx + iFtY - главный вектор касательных сил трения в комплексной форме; St - главный момент касательных сил трения

относительно оси шипа; 50ефе2я; -sZsL/2J -

область интегрирования.

Величина тангенциального напряжения pt для цилиндрического подшипника определяется на основании решения краевой задачи по известным формулам [58]:

ду ]у=о

-Р=21

1 др

(y=-%)-fp(l-f)Q. (6.68)

Здесь у - локальная координата, отсчитываемая по нормали к поверхности шипа.

Исходя из формул (6.66), (6.67) и (6.68) путем преобразования к безразмерным переменным, получим:

St = - paRL j j (ЯР -f ) dl; (6.69)

64-Е

Fit = -ipaRL-

(я/;+-з)еффС (6.70>

Здесь s (0 Ф 2я; -1 S +1) - область интегрирования для одного шипа; все прочие обозначения имеют прежний смысл.

Вычислим главный момент сил трения в случае ненагруженного радиального подшипника с шевронными канавками в предположении, что все условия применимости асимптотической теории выполняются. Ограничимся случаем, когда канавки образуют в профиле прямоугольную волну, т. е. ширина канавок равна

ширине выступов. Исходя из асимптотического представления решения краевой задачи для подшипника с шевронными канавками в виде суммы ряда (4.81) и удерживая в этой сумме первые два члена после подстановки его в (6.69) и интегрирования, получим

Ъщт{ 3ti(1-ti)cos (1 + т))бГ 1 + Зг)2

11(3+ Т1У sing \\

a]Jr

(6.71)

(6.73)

Т 4 [(1 + Ъг) cos а + (1 - T)S)3 sin (

Здесь ~ момент сил трения одного подшипника относительно оси шипа.

Для оптимальных значений (а = 66°; ti = 0,45), соответствующих максимальному запасу устойчивости, вычисления дают

St - 0,751 (6.72)

где itrt = -g--момент сил вязкого трения при отсутствии

канавок.

Рассмотрим влияние сил трения на перекрестные связи между подсистемами поступательных и вращательных движений ротора.

Предположим, что крутящий момент двигателя сводится к паре сил, инвариантной относительно выбора полюса приведения, тогда уравнения равновесия сил и моментов относительно оси шипа запишутся в виде:

St + S = Q.

Здесь все силы записаны в комплексной форме, причем F = = Fx + iFy - вектор гидродинамических сил давления; F = = Fxt + iFyt ~ вектор сил вязкого трения; Р = Fx + iFyb - вектор всех внешних сил; St - главный момент сил трения относительно оси шипа; - крутящий.момент.

Если привести все силы к оси подшипника, то первое уравнение не изменится, а второе примет вид

St + S.p~eyF,+e,F,y = Q, (6.74)

где Si - главный момент сил трения относительно оси подшипника.

Различие в моментах St и St имеет существенное значение в точных приборах, например гироскопах. Действительно разность St - St будет вызывать момент реакции опор подшипников, и если опоры не жесткие, то корпус машины будет поворачиваться вокруг оси подшипников.

Величина реактивного момента очень мала. Например, в гироскопах радиальная жесткость пары подшипников может достигать 168

с = 10 кгс/мкм. Если выбрать направление координатных осей OXY так, чтобы еу = О, то для радиального смещения получим оценку

Тогда из уравнений (6.73) и (6.74) будем иметь \St-St{ = \e.-F,y\-.

Если создается силой собственного веса ротора в 300 гс, то получим

\St - St\<

= 0,9-10-8 j-c-CM.

Влияние сил вязкого трения на величину главного вектора Fi незначительно лишь при ограниченных угловых скоростях собственного вращения ротора. Это видно непосредственно из выражения (6.70) для Fif в общем виде. Действительно, в силу ограниченности \Р\ и \Fi\ при очень больших угловых скоростях Q величина Ff \ может статьсоизмеримой по порядку с Pj , так как второй интеграл в (6.70) может увеличиваться с возрастанием Q беспредельно.

Однако, такие большие скорости соответствуют уже турбулентным режимам течения смазки и лежат в области неустойчивости типа полускоростного вихря. Практика показывает, что условие \Fit\< \Fi\ обычно выполняется.

33. Примеры расчета радиальных газодинамических подшипников с учетом требований к запасу устойчивости

Рассмотрим примеры расчета радиальных подшипников, которые наиболее интересны в смысле определения устойчивости движения по отношению к само возбуждающимся радиальным колебаниям.

Первые два примера относятся к машинам приборного типа, например гироскопам, опоры которых либо испытывают переменные нагрузки, либо вообще могут быть ненагруженными. Третий пример относится к машине с горизонтальным валом, радиальные подшипники которого находятся все время под постоянной нагрузкой собственного веса ротора.

1. В качестве первого примера рассмотрим расчет радиальных подшипников, работающих при малых нагрузках. Расчет должен производиться, исходя из условия устойчивости. При этом подшипники должны иметь стабилизирующие канавки, например шевронные.

Если угловая скорости вращения ротора Q и масса М приходящаяся на один подшипник, заданы, то дело сводится к определению оптимальных размеров D, L и геометрических параметров канавок. Как было показано в п. 28, оптимальные по критерию максимума запаса устойчивости геометрические параметры шевронных канавок могут быть определены заранее. При отношении ширины канавки к ширине выступа, равном единице, оптимальные параметры канавок таковы:

Число канавок п должно быть взято настолько большим, чтобы выполнялись условия применимости асимптотической теории (см. п. 18).

Отсюда видно, что для определения оптимальной глубины канавок необходимо знать минимальный зазор б. Зазор б должен выбираться как можно меньшим, причем нижняя граница определяется технологическими погрешностями и стабильностью геометрических форм. Действительно, если запас устойчивости измерять отношением массового параметра М к его критическому значению Му. (см. п. 28).

(6.75)

то из выражений для критической массы (6.9) и момента вязкого трения (6.71) можно установить, что при варьировании б и и фиксированных прочих параметрах, включая и коэффициент у, потери на преодоление момента трения будут тем меньше, чем меньше б.

Исходя из тех же соображений, можно установить, что длина подшипника должна быть максимальной, т. е. отношение Oq = = D/L должно быть как можно меньшим. Верхняя граница определяется конструктивными и технологическими соображениями. Вместо длины при расчете удобно задать параметр Од, тогда все дело сводится к определению Popt по заданным Mj, 7, Q, бщ, Оо, р после определения Popt находится Lopt-

Таким образом, задавая коэффициент запаса устойчивости у и минимальный допустимый радиальный зазор бп , можно вычислить оптимальную глубину канавок и оптимальный радиус шипа по прочим заданным параметрам.

При расчете оптимальных параметров по критерию максимума запаса устойчивости статические интегральные характеристики, такие как несущая способность и жесткость, могут оказаться недостаточными. В силу этого после расчета оптимальных по запасу устойчивости параметров необходимо сделать поверочный расчет статических характеристик. Если окажется при этом, что жесткость подшипников недостаточна, то следует уменьшить коэффи-170

циент запаса устойчивости у и произвести расчет заново. Уменьшение у приведет к увеличению Popt и повышению статической жесткости.

Рассмотрим авиационный гироскоп, схема которого приведена на рис. 17. В работе Паттерсона [46, т. 90, № 4 ] указывается, что радиальный подшипник имеет шевронные канавки. Но глубина их не приводится. Вычислим глубину канавок и коэффициент запаса устойчивости, предполагая, что профиль канавок имеет форму прямоугольной волны. Оценим также величину радиальной жесткости и момент вязкого трения.

За исходные данные примем следующие параметры радиального подшипника: L = 38 мм - длина подшипника; D = = 9,5 мм - диаметр шипа; М = 0,36 кг - масса ротора; й = = 24000 об/мин - угловая скорость; б = 1,75 мкм - средний радиальный зазор без учета канавок; р. = 1,82-10~* - коэффициент вязкости; Ра= 1 кг/см - атмосферное давление.

На основании этих данных рассчитываем массовые параметры М и М, определенные формулами (6.4), (6.10), при ЛЛ;;. Относительная длина подшипника Я, = 4; параметр Oq = 1/л = = 0,25; число сжимаемости

бцО R y 6- 1,8-10-Ц.2500.0.482

1,752.10-8

= 21;

безразмерная масса ротора

б \5 0,36(1,75.10-*)

981-1,82.10-20-0,952

= 0,036;

критическая безразмерная масса Xf 6,9

а ,35.

0,25-21

По формуле (6.75) находим коэффициент запаса устойчивости

0,036

м

1,35

0,027.

Этот запас устойчивости будет иметь место в том случае, если шевронные канавки имеют оптимальную глубину, соответствующую углу наклона aopt = 66° и параметру riopt = 0,45 при условии, что профиль имеет форму прямоугольной волны. Учитывая, что

Е (б + £) 1

найдем оптимальную амплитуду волны профиля Г1б 0,45-1,75 , .