ном состоянии на ротор действует постоянная гравитационная сила, уравнения малых колебаний будут несколько сложнее.

В этом последнем случае смещение во уже нельзя принимать малым, в силу чего функции, выражающие отображения смещений Ае и Ав£ в реакции AF и AF, следует варьировать в окрестности смещенного положения равновесия.

Дифференциальные уравнения малых колебаний для машины с газодинамическими подшипниками иной конфигурации (конические, цилиндрические и т. д.) будут иметь ту же форму, что и для сферических подшипников.

Действительно, если цапфы несферических подшипников имеют симметричные формы, т. е. несущие поверхности их являются поверхностями вращения, а ось симметрии цапф совпадает с осью фигуры ротора, то выбрав две точки О и О на оси цапф так, чтобы они располагались на одинаковом расстоянии от центра масс, мы можем привести реакции смазочного слоя к главным

векторам F, F и главным моментам, относительно точек О, О .

Формы поверхностей подшипников будут влиять только на

-> ->

структуру операторов, с помощью которых смещения в, е ото-

> > > >

бражаются в реакции F, F , S, SE .

При выводе уравнений мы всюду предполагали, что несущие поверхности цапф являются поверхностями вращения, оси симметрии которых совпадают с осью фигуры; это же относится и к несущим поверхностям подшипников.

В действительности реальные формы упомянутых поверхностей отклоняются от идеальных. Отклонения, обусловленные погрешностями изготовления, можно рассматривать как возмущения и учесть их в правых частях уравнений как переменные во времени возмущающие силы и моменты.

К этому следует добавить, что отклонение оси фигуры от оси симметрии эллипсоида инерции ротора также можно отнести за счет погрешностей несущих поверхностей цапф. Последнее обстоятельство позволяет учитывать статический и динамический дисбалансы совместно с погрешностями несущих поверхностей в виде эквивалентных внешних возмущающих сил и моментов.

7. Основные понятия устойчивости и виброустойчивости машин на подшипниках с газовой смазкой

Составной частью общей проблемы развития и применения подшипников с газовой смазкой является проблема обеспечения устойчивости и виброустойчивости роторов машин и гироскопов на газодинамических подшипниках. 52

Нормальный режим работы гироскопа или машины с газодинамическим подвесом ротора иногда называют режимом левитации . В таком режиме ротор вращается в газодинамических опорах без сухого трения, обусловленного механическими контактами между несущими поверхностями. Поддержание этого режима есть необходимое условие работоспособности подшипников с газовой смазкой в большинстве случаев. Исключение составляют некоторые гироскопы и слабонагруженные машины, подшипники которых при разгоне и остановке могут работать в режиме граничной смазки.

Нарушение режима левитации может произойти при чрезмер-

ных перегрузках, когда смещение \е\ ротора относительно подшипников будет соизмеримо с величиной рабочих зазоров.

Обычно подшипники рассчитывают так, чтобы они выдерживали заданную статическую нагрузку без нарушения нормального режима. В этом случае соответствующее статическое смещение должно быть меньше некоторого б-/ij, где К - наименьший

допустимый зазор; б - средний зазор при в = 0 [58]. Такой расчет еще не обеспечивает работоспособности подшипников машины или гироскопа, так как положение динамического равновесия может оказаться неустойчивым.

Обычно при потере устойчивости равновесного состояния центр масс ротора совершает периодическое движение с частотой, близкой к половине скорости вращения ротора.

Другими источниками возникновения колебаний центра масс ротора могут служить вибрации основания или удары.

Неустойчивость равновесного состояния должна быть исключена, так как при этом нарушается режим левитации. Но одной устойчивости недостаточно для работоспособности подшипников, так как при наличии значительных вибрационных перегрузок возможен механический контакт цапфы и подшипника. Последнее обстоятельство особенно опасно для гироскопов, которые обычно работают на-подвижных основаниях, испытывающих значительные вибрации.

Количественно виброустойчивость можно оценить амплитудой вынужденных колебаний ротора относительно статора, порождаемых вибрацией основания. В общем случае как устойчивость, так и виброустойчивость может быть исследована методами спектрального анализа по частотным характеристикам.

При исследовании колебаний ротора машин, даже в простейшем случае неподвижного статора, уравнения движения довольно сложны из-за сложности операторов, представляющих реакции газодинамических подшипников.

В рамках теории малых колебаний реакции подшипников могут быть приближенно выражены линейными зависимостями от векторов смещений ротора. В этом случае реакции можно определить с помощью передаточных функций. Например, для цилиндриче-

ского подшипника при малых радиальных колебаниях цапфы в окрестности центрального положения реакция AF представляется в виде

AF - Gip, i)Te, (2.42)

где AF = AFi + iAF; Ае = Ae + iAe - изображения по Лапласу соответствующих переменных, а р - параметр преобразования Лапласа по времени t.

Передаточная функция радиальной реакции G (р, i) играет особенно важную роль при исследовании возможных вихревых форм неустойчивости. Эта передаточная функция представляется в общем случае мероморфной функцией.

Таким же образом могут быть представлены реакции других типов подшипников.. Это представление весьма удобно получается на основе решения краевой задачи газовой смазки.

Для уточнения передаточных функций может быть применен метод гармонического баланса. Представление реакций подшипников с помощью передаточных функций открывает возможность применения к исследованию подшипникрв с газовой смазкой частотных методов. Заметим, что частотные методы можно применять к газодинамическим подшипникам и не пользуюсь передаточными функциями, а применяя к уравнению Рейнольдса метод гармонической линеаризации. По этому пути пошли Пэн [74] и Марш [72].

В дальнейшем не отдается предпочтения какому-либо одному из этих методов, а применяется комбинированный подход, сочетающий представления реакции через передаточные функции с последующим уточнением элементов частотных характеристик методом гармонической линеаризации. В соответствии с этим исследование устойчивости проводится с помощью известного критерия Михайлова-Найквиста. Применение критерия Гурвица к рассматриваемым здесь задачам затруднительно или вообще невозможно, так как приходится иметь дело с уравнениями довольно высокого порядка, имеющими комплексные коэффициенты.

Частотный критерий устойчивости Михайлова-Найквиста основан на принципе аргумента теории функций комплексного переменного.

Напомним формулировку этого критерия.

Если дано характеристическое уравнение А (р) = Р (р) + + Q (р) = О, причем функция Г (р) = Р (p)/Q (р) имеет т полюсов в правой полуплоскости комплексного переменного р, а все остальные в левой, то для устойчивости необходимо и достаточно, чтобы приращение аргумента функции 1 + Г (ico) при изменении со от -оо до -\-оо было равно -2пт, т. е. вектор годографа функции Г (ш) должен повернуться вокруг точки - 1+Ю ровно т раз. Если это условие не выполняется, тохарак-54

теристическое уравнение А (р) = 0 имеет корни в правой полуплоскости и, следовательно, система неустойчива.

При применении этого критерия для исследования устойчивости подсистем, описывающих колебания ротора ,в газодинамических подшипниках, встречается случай, когда функция имеет двукратный полюс р = 0. В этом случае частотный критерий требует уточнения в соответствии с принципом аргумента теории функций комплексного переменного.

Анализ распределения корней характеристического уравнения А (р) = О можно провести и по другому. Предварительно укажем, что для газовой смазки задачу о характере распределения корней уравнения А (р) = О можно заменить задачей о рас-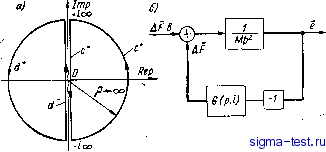

Рис. 13

пределении нулей функции V (р) = Мр + G (р, 0. т. к. структура рассматриваемых подсистем определяет тождество нулей функций А (р) и V (р). Функция V (р) имеет особенности, равные полюсам функции G (р, i), которые, как можно показать, лежат в левой полуплоскости комплексного переменного р.

На основании принципа аргумента можно заключить, что все нули функции V (р) будут лежать в левой полуплоскости, если число полных оборотов вектора V (р) вокруг начала координат в плоскости V при изменении р вдоль контура с =. с+ + с (рис. 13, а) в положительном направлении будет равно нулю.

Изменяя р вдоль контура с, будем считать число оборотов, которые при этом совершает вектор, изображающий функцию V (р), вокруг начала координат.

Будем сначала изменять р вдоль полуокружности С* бесконечно большого радиуса (рис. 13, а). Введем замену по формуле

р = р ехр {щ), (2.43)

тогда при р ->оо получим

lim V (р) = limMp ехр (12ф) + lim G [р ехр (/ф), t]- (2-44)

р >оо P-J-CO р->со

Ввиду того что на контуре функция G (р, i) не содержит особенностей, второе слагаемое в (2.44) ограничено по

модулю и

1 im V (р) = lim Мр2 ехр (12ф).

р->оо р->оо

(2.45)

Из равенства (2.45) видно, что при обходе контура вдоль модуль V (р) остается неизменным, а аргумент получает приращение, равное 2я.

Таким образом, вектор, изображающий функцию V (р), повернется в плоскости V на угол 2я против хода часовой стрелки, т. е. совершит один оборот вокруг начала координат.

Тогда, согласно принципу аргумента и критерия устойчивости по которым полное число оборотов вектора V (р) при обходе точкой р контура с = с+ + с должно равняться нулю, приходим к критерию, сходному с критерием Найквиста-Михайлова для систем с распределенными параметрами: для того чтобы система была устойчива, необходимо и достаточно, чтобы при изменении р вдоль мнимой оси от -4-too до -too число оборотов вектора V (р) по часовой стрелке вокруг начала координат равнялось единице.

Выделение области изменения параметров, определяющих устойчивость, может быть осуществлено с помощью известного в теории автоматического регулирования метода D-разбиения *.

Весьма полезными для исследования динамикрь газовых подшипников являются идеи и средства теории автоматического регулирования. Действительно, систему ротор-подшипники можно рассматривать как многомерную систему стабилизации положения вращающегося ротора относительно подшипников.

Каждую из подсистем можно рассматривать как отдельн1?1й канал системы стабилизации с обратной связью, в которой роль регулятора прямого действия выполняет смазочная пленка, а регулирующим воздействием является соответствующая составляющая силы реакции.

В этой схеме смазочную пленку можно рассматривать как бесконечномерное континуальное звено с интегральными выходами по нескольким каналам.

Отдельные каналы в общей структуре являются двухмерными и представляются комплексными уравнениями.

Так подсистема, описываемая уравнением (2.40), выступает как канал стабилизации центра масс ротора в его экваториальной плоскости по координатам и е, эквивалентным одной комплексной переменной е = -\- ie. Эквивалентная структурная схема (рис. 13, б) содержит два звена: объект стабилизации с передаточной функцией ММр и регулятор с передаточной функцией G (р, t). Это соответствует уравнениям канала:

уй(-Дв); A> = -G(p,t)e,.

(2.46)

* Теория автоматического регулирования. Под ред. Солодовникова. Кн. 1. М., Машиностроение, 1967. 768 с.

Здесь е, Ар, AF - изображения по Лапласу, р - оператор преобразования Лапласа по времени t; G (р, t) - комплексная передаточная- функция смазочной пленки как эквивалентного регулятора соответствующего канала.

Исходя из этого представления, получаем передаточную функцию эквивалентной разомкнутой цепи стабилизации, равную

Г(Р) = 4- (2.47)

Точно так же можно построить структурные схемы и найти соответствующие передаточные функции эквивалентных разомкнутых цепей для всех прочих подсистем.

Для исследования устойчивости и виброустойчивости подсистем типа (2.46) следует исходить из амплитудно-фазового критерия для комплексных передаточных функций. Особенностью применения этого критерия к комплексным передаточным функциям является то, что годограф частотной характеристики будет уже несимметричен относительно вещественной оси, так что его следует строить для всего диапазона изменения: р = гю; -ю < < ю < + оо.

8. К вопросу о влиянии перекрестных связей на устойчивость ротора в газодинамических подшипниках

Обозримость и простота результатов исследования устойчивости ротора в газодинамических опорах зависят от упрощений, и, в частности, от разделения замкнутой системы на подсистемы. При этом приходится пренебрегать перекрестными связями, в состав которых могут входить и линейные.

В данном параграфе рассматривается способ, позволяющий учитывать влияние линейных составляющих перекрестных связей между подсистемами на устойчивость связанной системы.

Дальнейшее исследование динамики роторов в подшипниках с газовой смазкой базируется на том, что при малых движениях ротора в окрестности равновесного положения вариации составляющих реакций Af и AS могут быть представлены линейными операторами. Относительно этих операторов еще предполагается, что они допускают применение преобразования Лапласа. Другими словами, предполагается, что вариации реакций подшипников AF, Af и Afg выражаются через передаточные функции.

В общем случае эти выражения записываются в виде:

Afg = Af,=

аК =

- Gil - Gi2 Аг - Gi3 Ae;

- G21 Ae. - G22 Ae - G23 Ae~;

- G31 Aet - Ggj Ae - G33 Aej,

(2.48)