Умножая пОчлёНйо последнее урабйёние на Ф* и интегрируя в пределах от -1 до +1, получим в силу условия ортогональности (4.47)

откуда найдем

4а (-1)

К2зг(2/-1)а2(г

/= 1, 2, 3,...

(4.49)

Подставляя эти коэффициенты в (4.48), найдем искомое аналитическое представление функции / {Q в виде суммы ряда Фурье

4а V (-1)

Здесь

И, = 90- -(2/-1)-Ро

ла (2j / =1

1)

cos(2/-l)S.

(4.50)

где .И-; Ро = .

Сумма ряда (4.50) сходится абсолютно и непргерывио при всех значениях параметров. Быстрота сходимости зависит от величин параметров: при малых х = Хо/ сходимость лучше, чем при больших.

Не останавливаясь на анализе распределения давления, что можно было бы сделать исходя из (4.44) и (4.50), перейдем к вопросу о влиянии числа канавок п, угла наклона а и других параметров канавок на несушую способность упорного подшипника. Для вычисления несушей способности упорного подшипника с шевронными канавками согласно (4.43) и (4.44) будем иметь

1 2я

nDLpa

2п J о

о L

+(Re {/ 1-4--

-i-Rei/ e-i + 1

2Н J

do), (4.51)

где Я = 1, - т] cos со, а / определяется формулой (4.50). Вычисляя интегралы, получим:

1 -f-co

1 ( !)/-! Sin (21-1)?

3i\dt,\h (?i) - u,-(2/- 1) L

° 1 +1

(3 = j 1 / i* = I u.2(2/ - 1)

0 /=1

2 (- 1)

3X(2/-1)

Для Исследования влияния отдельных параметроЁ подшипника на несушую способность его рассмотрим асимптотические свойства интегралов и ез- Прежде всего обратим внимание 4ia соб-

ственные числа [iy. Внося (fi под знак суммы, мы получим в знаменателях отдельных слагаемых множители ар, и а*р,/. Преобразуем эти множители следующим образом:

(2/-1)а -роо

Учитыбая выражения для и Ро, найдем, что

aV; = - 1 - Г-f - (2/ - 1) о- tgaf + ix.

(4.52)

Величины о и X убывают с увеличением п обратно пропорционально числу канавок, в то же время величина ор,/ остается ограниченной при фиксированном /. В пределе при /г -> -}-оо будем иметь

lim = - 1 - tg а= - . (4.53)

Очевидно, что это верно лишь для конечных значений /, Хо. Оо, а > 0.

Возвращаясь к (4.50), заметим, что в силу (4.53) имеет место асимптотическое представление

Л->--оо

/ =1

Существенно, что предельное выражение, аналогичное (4.53), можно получить и другим путем, не связывая его с числом канавок п,

lim аХ = - 1 - tg а + IX = - + iX- (4.54)

Это выражение, как и (4.53), может быть определено лишь при ограниченных /, но при любых х- Уменьшение параметра а возможно не только за счет увеличения числа канавок, но и за счет уменьшения геометрического парамет)а а = DIL, т. е. за счет увеличения поперечного размера полосы, что эквивалентно в случае цилиндрического подшипника увеличению его длины L. Далее, заметим, что ряды, с помощью которых представляются интегралы i, , , -быстро сходящиеся.

При достаточно малых а будем иметь приближенные выражения для интегралов:

(1 - ix-cosa)

2 (2/-/=1

1-(-1)-Чш(2/-1)?

2 n2(i ,-cos2a) Zj(2/-1

+ C0

1 cos g у

G/3~ л2(1 +xcos a) Zj

2(-1Г я(2;-1) J

, a>0.

Суммируя ряды, получим при о -> о асимптотические значения интегралов в виде:

- (x cos a

г -2(1 -txcosa)

(4.55)

Рассмотрим теперь асимптотическую несущую способность. Для этого найдем из (4.55) следующие интегралы:

Re {/ ) dl = Re {с?хк=о = .gf ;

Im {/ ) dl = Im {drx}j=o = 1 jgt ;

imi.Hg-- 2(iygco°;. :

Подставляя эти интегралы в (4.51), получим асимптотическое выражение несущей способности упорного подшипника

/2 cos* а

cos (О rfco 1 - г\ cos (О

1 4 т , 2cos4a J 1 -ncoSM 4 l+Xcos*aJ 1 -ticosm

О = tga; a>0.

Вычисление оставшихся интегралов не представляет труда и окончательно получим

F Зт1 + 4(1 -К Г) xcos* nDLpa aYT l + Xcos*a

% sin 2a

(4.56)

Напомним смысл величин, входящих в эту формулу. Левая часть выражает удельную статическую реакцию подшипника, приходящуюся на единицу площади и отнесенную к атмосферному давлению ра- Площадь модели упорного подшипника равновелика площади поверхности радиального подшипника радиуса R и длины L. В правую часть (4.56) входят геометрические параметры т], а, а и так называемое число сжимаемости зависящее от геометрических параметров подшипника и физического состояния смазочной среды. В этом случае

Перейдем к анализу формулы (4.56). Прежде всето из нее вытекают все результаты работы Уилдмена [46, т. 90, № 4].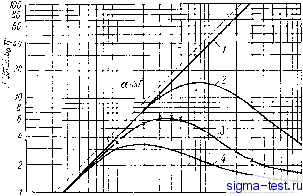

20 40 60 ( Рис. 24

200 mm юоол

а

В этой работе данная задача решалась методом малого параметра в предположении, что т] < 1, В результате расчетов на ЭВМ были построены графики зависимости несущей способности от числа сжимаемости при различных значениях геометрического параметра т) < 1.

Для того чтобы привести формулу (4.56) в соответствие с графиками работы Уилдмена [46, т. 90, №4], показанными на рис. 24, необходимо в ней произвести упрощение, основанное на допущении, что т] < 1. В результате упрощения получится формула, которая в наших обозначениях имеет вид

5 /2 cos* а

X sin 2а

t\nDLpa 4 l + xcos*a 8 a(l + xcos a) (

Положив в (4.58) х = оЛ; а = а* 12л (где а* в работе Уилдмена есть отношение длины канавки к ее ширине, названо числом подшипника, вычисленным по его ширине, обозначенной через а), можно убедиться, что результаты расчета, проведенные

для а = 50° и о* = 0,5, соотбетствуют графику Уилдмена (кривая 3 на рис. 24). На рис. 24 обозначено пунктиром решение Уиппла, сплошной линией -решение Уилдмена для различных значений 1/а*: / -0,01; 2 -0,2; 3 -0,5; 4 - 1,0.

Формула (4.56) дает более обший результат, так как она справедлива во всем диапазоне изменения числа сжимаемости х при любых а, удовлетворяюших условию tg а > а. Кроме того, при X- -}-оо из (4.56) получается более точное значение несушей способности.

Из формулы (4.56) вытекает, что в подшипнике с шевронными канавками при а > О имеет место эффект поперечного нагнетания. Этот эффект выражается вторым членом, который при определенных условиях значительно превосходит первый, выражающий обычный продольный эффект смазочного клина. Поперечный эффект нагнетания при прочих равных условиях тем больше, чем больше ширина полосы и число канавок п, т. е. чем меньше о = а J п.

Как показано в работе Уилдмена, при достаточно малых х и о, продольным эффектом можно пренебречь. В этом случае формула (4.56) упрошается и принимает вид

F 3 ri X sin 2а

nDLpa

8 YY а (1-fxcos* а)

(4.59)

На основании (4.59) можно установить, что для постоянных д и а максимальный поперечный эффект достигается при Хт = 1/cos а. Подставляя это значение в (4.59), получим:

nDLpa 8 j/ ! Оо

tea.

(4.60)

При X С Xm = 1/cos а эффект увеличивается монотонно, приблизительно пропорционально увеличению х = tJn.

Произведем оценку максимальной удельной несущей способности, когда rt = 8; а = 45°; Oq = 0,5; ц = 0,6.

Подставляя эти значения в (4.60), получим

fmax 2-3-0.6-8 nDlpa 8 J/ ! - 0,6

= 2,7.

Соответствующее число сжимаемости, при котором достигается максимум, будет равно:

0,5 -

Вычислим теперь первый член в (4.56)-, выражающий продольный эффект,

3-0,6+ 4(1 - )/ 1-0,6) 4-0,25

41/ 1-0,62

1 + 4-0,25

: 0,29.

Таким образом. Даже при сравнительно малом числе каНавок. (п = 8), поперечный эффект превосходит продольный и составляет около 89% от полной несущей способности..

При больших значениях я вклад поперечного эффекта в общую несущую способность будет еще больше превосходить соответствующий вклад продольного эффекта, если параметр х не слишком велик. На этом Свойстве шевронных спиральных подшипников основана теория узких канавок, разработанная в своем первоначальном виде Уипплом 156], в которой предполагается, что при большом числе канавок можно не учитывать продольный эффект. Согласно этой теории несущая способность монотонно возрастает с увеличением числа сжимаемости, в действительности это имеет место лишь при достаточно малых значениях числа сжимаемости. Из (4.59) видно, что верхняя граница применимости теории узких канавок определяется максимум F (х) и при этом % должно удовлетворять требованию

Хо <

cos а *

(4.61)

В действительности это условие должно выполняться с некоторым запасом, так как вблизи точки максимума несущей способности погрешность теории Уиппла будет значительной (рис. 24).

На основании вышеизложенного можно сделать следующие предварительные выводы.

Подшипники с шевронными или спиральными канавками характеризуются эффектом поперечного нагнетания, который исчезает при нулевом угле наклона канавок (а = 0).

При большом числе канавок п, когда а = Оо/л < tga, распределение давления в подшипнике приближается к асимптотическому, которому отвечает решение краевой задачи при п -> +оо.

Это асимптотическое решение может быть найдено из (4.43) в результате предельного перехода. Действительно, из (4.43) имеем

Р 1 = ii{/ e-. cosa,}Ч--(Rei/ }-

l/ lO-W

Im {/ } dl.

(4.62)

Из (4.50), учитывая (4.53) при п получим асимптотическое выражение

; Хо

+00 и Хо/<о = const,

COS а.

(4.63)

Подставляя это выражение в (4.62), получим асимптотическое выражение для давления, которое с точностью до членов О {v)