где A = Ue{,}; В = \т{,]; = 1

th</

зазора

Полученная формула дает аналитическое представление главного вектора сил давления, действующих со стороны смазочной пленки на шип. Формула позволяет рассчитать как несущую способность цилиндрического подшипника, так и угол нагрузки. Несущая способность определяется модулем, а угол нагрузки- - аргументом комплексного.выражения (4.26). При расчете по формуле (4.26) возникают лишь некоторые трудности, связанные с вычислением величин А и В, которые зависят от двух параметров подшипника сго и Хо; эти трудности легко устранить табулированием функции (1 = 1 {Оо, Хо) (см. приложение 2).

Сопоставление результатов расчета несущей способности и угла нагрузки по этой формуле показывает хорошее совпадение с результатами в работе [57] (см. приложение 3).

17. Решение краевой задачи статики для цилиндрического подшипника с шевронными канавками, имеющими синусоидальный профиль

Как известно, цилиндрические подшипники с гладкой поверхностью при малых радиальных нагрузках не обеспечивают достаточного запаса устойчивости [58]. В связи с этим, в машинах малой мощности, а также при вертикальном положении вала применяются профилированные подшипники. В настоящее время все более широкое применение находят подшипники сО спиральными канавками. Первая теоретическая разработка упорного подшипника со спиральными канавками была опубликована Уипплом в 1949 г. Методика, предложенная Уипплом, применяется для расчета и радиальных подшипников с шевронными канавками, имеющими прямоугольный профиль. В более поздней работе Вора и Чау дается теория идеализированных подшипников со спиральными канавками произвольной геометрии. В этой работе, а также в ряде других решение задачи не является равномерно точным для всех значений параметра сжимаемости и пригодно лишь для достаточно малых значений этого параметра. Этот вопрос подробно анализировался в работах Уилдмена [46, т. 90, № 4], Константинеску и Кастелли [46, т. 91, № 1].

В данном параграфе мы рассмотрим краевую задачу статики для цилиндрического подшипника с шевронными канавками при нулевом эксцентриситете (е = 0), что соответствует случаю, когда подшипник свободен от нагрузки. Постановка задачи остается такой же, что и для гладкого подшипника (см. п. 15).

На рис. 22 изображена опора длиной L: а -с шевронными канавками (Li = L); б -с частичным профилированием {L, < < L); в - выбор начала координат. В этом случае функция 94

Я = 1-Т1С08(Пф4-Р9,

(4.27)

где Р = Posign С (Ро = const); у] = щгё ~ относительная амплитуда изменения глубины канавки; Ро =---ntgct-коэффи-циент, характеризующий наклон канавок; п - число канавок; а - угол наклона канавок к образующей; Е - амплитуда профиля синусоидальных канавок, равная половине их глубины; =zj~L-относительная координата, отсчитываемая вдоль образующей шипа от средней линии = 0. , Учитывая сим-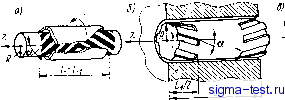

Рис. 22

метрию, будем решать краевую задачу, выраженную уравнениями (4.1), (4.2), для одной половины подшипника (О < 1). В этом случае граничные условия (4.2) можно заменить такими:

ЦТ Я=+ь ;=о = 0; ф = ф+2 Г

Второе условие не относится к специальному случаю, когда профилированные зоны смыкаются в точке = О (рис. 22, с). В формуле (4.27) следует положить р = Pq. Применяя обобщенный метод ЯЯ-линеаризации, решим задачу в первом приближении. Опуская промежуточные рассуждения и выкладки, которые будут такими же, как и в п. 15, сформулируем задачу 1-го приближения в комплексной форме. Для этого определим комплексный зазор, соответствующий формуле (4.27):

= 1 -У]е-

t(x>

(4.28)

где (О = мф -f РС.

Краевая задача, соответствующая (4.8), (4.9), с учетом новых граничных условий, преобразуется к виду:

JU + а1Жц - %оЖ; = fXo Tie- ; Ж 1=1 = 0; Ж1 j=o = 0; Ж\ц, = Ж ф+2л-Решение уравнения (4.29) будем искать в форме

(4.29) (4.30)

(4.31) 95

Подставляя (4.31) в (4.29) и учитывая (4.30), получим одномерную краевую задачу для / (Q:

/;-2ф /;-(-Ь + р§) / =4-;

Д(0) = 0; / ( ! 1) = О,

Хо . о tgg -ТГ- > Ро - -Z-

(4.32)

Эта линейная задача может быть решена в конечном виде

(4.33)

(4.34)

В отличие от подшипника с гладкой втулкой, в случае шевронного профиля решение 1-го приближения (4.33) получается довольно сложным, поэтому в следующем параграфе мы займемся анализом уравнения (4.32) другим способом.

Заметим, что для цилиндрического подшипника с синусоидальным профилем при нулевом угле наклона (а = 0) из (4.33) получается решение вида (4.14)

Рассмотрим теперь 2-е приближение. Для вычисления поправки снова обращаемся к уравнению (3.55). В данном случае ф О и уравнение (3.55) будет иметь вид

Граничные условия для А () должны быть нулевыми, так как решение первого приближения Wi удовлетворяет граничным условиям точно. Для области 1 1 ==с 1 имеем

А(0) =А(+1) = 0. Интегрируя (4.35) два раза, получим

(4.36)

о 11.

После нахождения произвольных постоянных это выражение примет вид

2л I 2л

АХО =

(H - YW) йф +

4я .

dZ\WWid(p. (4.37)

Учитывая (4.28), сделаем замену переменной интегрирования по формулам:

Ф = 4-(со-Ш; = ф=-4. (4.38)

В результате получаем

А(9 = ХЯ -ВДЙсо-d?№dco. (4.39) о £0

где Я = 1 - т] COS ю; ю = Пф -f pg; О < ? < 1.

При ? = О следует полагать Р = О, тогда выражение (4.39) будет справедливо в замкнутом промежутке О 1. Эта особенность объясняется тем, что функция зазора Я терпит разрыв 1-го рода в точке- S = 0.

Для того чтобы вычислить поправку А (Q окончательно, необходимо подставить в (4.39) решение 1-го приближения Чц которое согласно (4.33) имеет выражение

,=.НцКе[!Л)е- }, (4.40)

отсюда можно получить

= 4- [4 + ri (1 + ЫГе- + ril + ГпГ е +

+ 4т1 (1 +/ ) е- + 4т1 (1 + /;) е + 2ti] 1 + / f]. (4.41)

Здесь fn -сопряженная комплексная функция. Подставляя это выражение в (4.39) и вычисляя интегралы, получим

1т/ Мф, (4.42)

где р = Ро > О при О < ? < 1 и р = О при g = 0.

Первое слагаемое в полученном выражении соответствует поправке к решению в случае подшипника с гладкой втулкой, но отличным от нуля эксцентриситетом (см. 4.18), а второе слагаемое характеризует эффект поперечного нагнетания.

Полное решение во втором приближении запишется в виде

% = + А (9 = 1 - т] cos 0) + Т1 Re if (О е--) +

+ Ч\ ( Re {fn (D) - 4- 1 fn (Q I) - -f P 1 1/. (01 d

p = po; 0<g<l; 0<ф<2я. (4.43)

В этом решении со = Пф -f pg, а / (t) определяется выражением (4.33). Напомним, что здесь мы получили решение для случая несмещенного шипа, когда е = О, однако оно позволяет вычислить важнейшие статические и динамические характери-

7 в. и, Дроздович 97

стики -статическую и вихревую жесткость подшипника (см. гл. V). Кроме того, полученное решение пригодно для исследования упорного кольцевого подшипника с шевронными канавками, точнее, его модели в виде прямолинейной полосы бесконечной длины. Такой моделью пользовался Уилдмен [46, т. 90, № 4] при исследовании упорного подшипника с шевронными канавками.

Можно показать, что все результаты этой работы вытекают из данного решения.

18. Качественное исследование упорного подшипника с шевронными канавками

Рассмотрим модель упорного подшипника, образованную разверткой концентрически расположенных несущих поверхностей радиального подшипника. На рис. 23 показаны упорный кольцевой подшипник с шевронными канавками и его модель: а - упорный диск; б - развертка диска в полосу (видхверху); в - продоль-

у/огарисрмттая спирало выступ

НаиаШ

Рис. 23

ный разрез полосы подшипника. Для этой модели будут справедливы все результаты, полученные в предыдущем параграфе, если мы потребуем, чтобы скорость скольжения верхней полосы с гладкой поверхностью была равна окружной скорости шипа V = QR. В этой модели угол ф будет играть роль безразмерной координаты, а радиус R - роль единицы масштаба.

Результирующая сила давления смазочного слоя на верхнюю пластину длиной 2nR = 2ягв и шириной L = Га -ri может быть вычислена по следующей формуле:

nDLpa

(4.44)

где можно взять из (4.43); область интегрирования S заключена в пределах: -ls;cs£;+l; 0=££фй£ 2п.

Расчет несущей способности по формуле (4.44) целесообразно делать на ЭВМ, несмотря на то что все интегралы вычисляются

й конечном виде. Именно этим путем производилось исследование упорного подшипника Уилдменом на базе решения уравнения Рейнольдса методом малого параметра [46, т. 90, № 4].

Для качественного исследования удобно, по крайней мере на первом этапе, иметь аналитические представления основных характеристик подшипника. Для того чтобы найти аналитическое представление несущей способности и жесткости упорного подшипника желательно прежде всего, упростить выражение (4.33) для функции / (Q. Такое упрощение может быть получено путем разложения функции / {I) в ряд по собственным функциям оператора дифференциального уравнения (4.32).

Рассмотрим для этого следующую вспомогательную краевую задачу типа Штурма-Лиувилля:

X (Ф) = Ф - 2фоФг - гФ = иФ;

Ф : 2 = Ф ;+2,

(4.45)

где р - произвольная константа.

Соответствующие краевой задаче (4.45) собственные функции и собственные числа будут таковы;

k = 0, ±1, ±2,...

(4.46)

(2fe-i)-p;

Собственные функции Ф (Q удовлетворяют следующим условиям ортогональности:

(Фь Ф/) f Ф,ф; = Р Р = (4.47)

-1 [ О при кф ].

Здесь Ф/ {Q - сопряженная комплексная функция по отношению к (9.

Принимая собственные функции (4.46) в качестве координатных, представим искомое решение уравнения (4.32) в виде суммы ряда

/ (Q= ЕаДФ; + Фу-1). (4.48)

Легко видеть, что каждый /-й член этой суммы удовлетворяет граничным условиям: S = 0; =

Подставляя (4.48) в (4.32) и учитывая (4.45), получим в силу линейности оператора

fn ® = S а/ (5Ф/ + 5Ф1-/) =

2 /(1/Ф, + Щ ,Фм) =