мация действительного профиля толщины смазочного слоя Н

некоторой функцией Я, непрерывной и гладкой во всей области интегрирования, тогда решение получаегся сразу для всей области с Ъомощью условий (3.13), (3.14). Примечательно, что если построить некоторую последовательность аппроксимирующих функций Я, имеющую своим пределом кусочно-непрерывную функцию Я, то соответствующая последовательность решений уравнения Рейнольдса при % < оо, S < оо сходится именно к тому решению, которое получаегся упомянутым выше способом сращивания давлений и расходов на линиях разрыва функции Я и ее производ-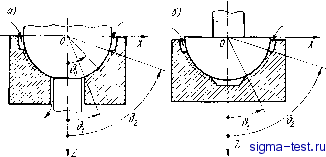

Рис. 16

ных. Таким образом, .подтверждается, что конечные разрывы функции Я сами по себе не нарушают непрерывности эпюры давления. Учитывая это обстоятельство, а также имея в виду, что различия в давлениях, рассчитанных для тонкого слоя с помощью уравнения Рейнольдса и на основании более точных уравнений Навье-Стокса, локализуются вблизи ступенек и изломов *, можно непосредственно искать единое решение уравнения Рейнольдса с кусочно-непрерывными коэффициентами, охватывающее всю область интегрирования, без выделения разрывов в качестве особых линий. Этот способ применяется довольно часто, и результат получаегся тот же, что и при использовании условий сращивания (3.15), (3.16). Однако гораздо удобнее иметь дело с непрерывными и дифференцируемыми функциями толщины слоя, с помощью которых можно аппроксимировать кусочно-непрерывную функцию и получить решение с любой желаемой степенью точности. Такие гладкие функции обычно и будут использоваться в дальнейшем.

В заключение рассмотрим два характерных примера конструкций сферических подшипников и сформулируем для них граничные условия к основному уравнению (3.11).

* При условии, что расстояние между соседними ступенями или изломами (например, ширина спиральной канавки) - весьма большая величина по сравнению с толщиной смазочного слоя (хотя она может быть малой по сравнению с размерами подшипника).

1. Вентилируемый подшипник (рис. 16, а) имеет несущую поверхность в виде сферического пояса 9 Q, который сообщается с окружающей атмосферой как со стороны экватора, так и со стороны полюса. Часть несущей поверхности подшипника, расположенная между параллелями Эц и Q{%Q,), профилирована спиральными микроканавками или ступенями Рэлея. В последнем случае соседние секции ступенчатого профиля разделены глубокими вентиляционными канавками, направленными по меридиану. Рассматриваемым опорам соответствуют граничные условия:

Р/е=е. = е=е = 1;

Р(Ф, 9, 0 = Р(ф + 2л, 9, t); = 1, j= О, 1, Л-1,

(3.18)

где N - число секций профиля Рэлея (шириной вентиляционной канавки, можно пренебречь по сравнению с протяженностью секции по углу ф). Последнее условие может относиться лишь к профилированному поясу 9о <9 <92. В пределах непрофилиро-ванной части несущей поверхности следует пользоваться вторым выражением (3.18).

Если несущая поверхность профилирована спиральными канавками, то она обычно состоит из двух поясов: профилированного (называемого иногда зоной нагнегания) и непрофилированного (называемого зоной утечки). Решение уравнения (3.11) можно искать отдельно для профилированного и непрофилированного поясов (хотя это не обязательно), тогда согласно (3.15), J3.17) задаются следующие дополнительные условия на их общей границе 9 = 9о:

-Р/е=е -о = Р/е=е +о;

(hJ) .(3.19)

2. Рассмотрим подшипник, не имеющий полюсного отверстия (рис. 16, б), его профилированный пояс 9 = 9 = 92 через свою верхнюю границу сообщается с окружающей атмосферой, а нижней границей примыкает к закрытому объему О 9 9. Условия (3.18) остаются в силе, только первое из них относится лишь к сечению 9 = 92. Если толщины зазоров в областях О < 9 и 9i < 9 ==s 92 соизмеримы (закрытый объем можно рассматривать как часть смазочного слоя), то, к упомянутым условиям следует присоединить условие ограниченности решения на полюсе Р е=о = = Л < оо (Л -некоторая положительная величина), которое в случае чисто осевой нагрузки заменяется условием

эе/е=о~

Можно также задать дополнительные условия (3.19) в сечении Э = 01. Если же толщина зазора в закрытом объеме много больше, чем в профилированной зоне, то во всем объеме, включая граничное сечение 6 = 6, давление близко к постоянной величине. Эта неизвестная константа может быть определена из условия сохранения массы газа в рассматриваемом объеме, которое представим в форме интегрального условия, выражающего равенство нулю массового расхода через сечение 0 = Gj.

Учитывая (3.16) и (3.17), а также изотермическое соотношение р ~ р, получим

Поскольку уравнение Рейнольдса (3.11) нестационарно, то, помимо граничных условий, основные разновидности которых были рассмотрены выше, его решение в общем случае должно подчиняться и некоторым начальным условиям, описывающим распределение давления или других связанных с ним величин вдоль смазочного слоя в момент времени т = 0.

12. Краевые задачи газовой смазки для цилиндрического, плоского, кругового и конического подшипников

В гироскопах часто используются газодинамические опоры катушечного типа, образованные одним цилиндрическим радиальным подшипником и двумя плоскими упорными (рис. 17).

Сформулируем краевую задачу газовой смазки для цилиндрического подшипника. Чтобы получить основное уравнение типа (3.11) для цилиндрического подшипника, можно было бы повторить весь выводп. 10, записав исходные уравнения (3.2)-(3.5) в цилиндрических координатах. Однако тот же ре-Pjji, jy . зультат можно получить,

исходя непосредственно из уравнения (3.11). Действительно, рассмотрим весьма узкий сферический поясок шириной L и радиусом R, расположенный симметрично относи-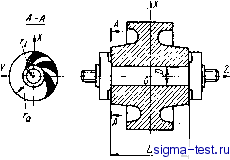

тельно экватора

в области -g--

:0 =

2 и wv/.jiuv j л 2 с 2 (рис. 18). Очевидно, что при достаточно малом е такой поясок можно приближенно рассматривать как часть цилиндрической 78

\

поверхности. Из соотношения z R {-В). справедливого при \z\ R, где г - осевая координата, следует, что

51П9Я=:1.

Учитывая эти преобразования, переходя к безразмерной осево Хдинате =L/MIU < 1). а также вводя обозначение а -= 2R/L, получим из (3.11)

djHP) дх

(3.20)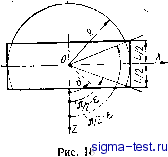

Подробный вывод этого основного уравнения газовой смазки цилиндрического подшипника можно найти в [58; 25]. Уравнение для безразмерного, зазора Я в случае чисто поступательных смещений вала может быть получено из уравнения (3.12), если положить в нем Э:

Я = 1-8;С08ф-8у sin ф-f Т]Ы (, ф).

(3.21)

Выражения для окружной и осевой составляющих скорости газа в смазочном елок цилиндрического подшипника аналогичны формулам (3.6):

Наиболее типичные граничные условия к уравнению (3.20) в соответствии с (3.13) и (3.14) запишутся в виде: Р/£=±1 = I-; Р/ф = Р/ф+2я.

Для плоского кругового упорйого подшипника основное уравнение в полярных координатах г, ф также получится из уравнения (3.11), есЛи рассмотреть последнее в окрестности одного из полюсов сферы радиуса (0 = 0 или 0 = я). Например, в окрестности точки 0 = 0 можно положить:

sin9 =

тогда из (3.11) следует

ат(5?) + 4(*1) =

г2 / d(HP) . d(HP)\ Эф dt J

(3.22) 79

а выражение (3.12) при осевых смещениях ротора принимает вид(9 1)

Я= 1-е, + т1м(г, ф). (3.23)

Заметим, что радиус R в уравнении (3.22) играет роль формаль ного масштаба и может быть выбран произвольно (x/R не зави сит от R и, следовательно, фактически R не входит в уравнение) Граничные условия к уравнению (3.22) могут быть сформули рованы по аналогии с соответствующими условиями для цилиндри ческого подшипника как частное следствие условий (3.13), (3.14).

С помощью аналогичных приемов можно получить уравнение Рейнольдса для конического подшипника. Будем рассматривать поверхность короткого конического подшипника (рис. 19.) как предельное положение поверхности сферического пояска 9-0Q]=ie при е -> О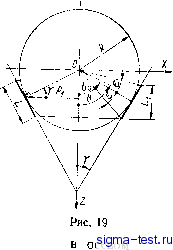

% = -о--У,

(3.24)

его длина

где у - угол полураствора конуса. Пусть R - радиус сферы; R = = COSY - средний радиус конического подшипника; L - длина подшипника по образующей; - направлении. Тогда, вводя обозначение

(3.25)

получим следующую связь между полярным углом В и линейной координатой с маштабом L/2, отсчитываемой вдоль образующей конуса от линии касания со сферой к его вершине (или, что то же самое, относительной осевой координатой Z = 2z/Lj)-

9 = 60-- (о 1).

Учитывая, что согласно (3.24) и (3.26)

аё -оч; sm0;= coS7--77

(3.26)

siny.

получим из (3.11) следующее уравнение:

а-Л I) + Ч- I-- 4 v) ai [ (cos V -

д(НР) дт

JCI<1.

(3.27)

При a

00 уравнение (3.27) упрощается и принимает вид 4,(я.р,) + а.сов.,Л(я.р)-

= cos7

д{НР) д(НР) Л Эф дт

(3.28)

Граничные условия для конического подшипника аналогичны таковым для цилиндрического и сферического.

Выражение для безразмерного зазора Н между несущими поверхностями конического подшипника при поступательном смещении шипа получается из (3.12), если сделать замену:

sin9j= coS7; cos9j= sin7,

которая следует из (3.24) и (3.26) при о - схз,

Н = 1 - (ехС05ф-(-еуз1пф)С08 7 - егтуу)и (, ф). (3.29)

Выражения (3.21), (3.23) и (3.29) справедливы лишь при отсутствии угловых перемещений оси вала относительно подшипников.

Заметим, что способ вывода уравнений (3.20), (3.22) и (3.27) как частных следствий уравнения (3.11) не позволяет обосновать области определения соответствующих дифференциальные операторов, так как в основе его лежит допущение о малой протяженности одной из криволинейных координат. Более полный и строгий вывод можно было бы получить, исходя йз уравнений движения газа в векторной форме (Пэн [53, т. 85, № 2; 75]).

13. Аналитическое представление толщины смазочного слоя при угловых рассогласованиях осей шипа и подшипника

Величина зазора между несущими поверхностями опор (за исключением сферических) зависит не только от поступательных перемещений шипа, но и от угловых перемещений его оси. При угловых перемещениях обычно возникает восстанавливающий момент реакции смазочного слоя.

Рассмотрим коническую опору (рис. 20), с которой свяжем три декартовые системы координат: OXYZ, От), OiXYiZ, где О - центр сферы радиуса R, касательной к несущей поверхности конического шипа в точках окружности, которая делит образующие пополам; Oi - центр сферы радиуса Ri > R, аналогичным образом связанной с несущей поверхностью подшипника. Соответствующие оси систем OXYZ и OXiYiZi параллельны и их направления фиксированы, а ось t, системы Olxit, направлена по оси вращения шипа. При совмещении центров О, 0, а также продольных осей шипа и подшипника всетрисистемы координат совпадают, а функция распределения толщины смазочного слоя зависит только от профиля несущей поверхности подшипника (поверхность шипа считается строго конической и абсолютно гладкой). Изменение этой функции может быть обусловлено как поступательными