и исключая ASi из (5.42) с помощью (5.41), получим: / Q2 , , г? iKo

PaRL 2х

S А[/ =

=-Gi(s, i)At

PaRL

(5.44)

Это уравнение аналогично уравнению (5.35). Так же, как и раньше, вместо G (s, i) рассмотрим его асимптотическое представление, справедливое при малых а, т. е. для достаточно длинного подшипника

Эта формула по структуре аналогична (5.36). Из (5.26) получаем

1 + s-iXo

W{s, I, i)

(5.45)

(5.46)

Подставляя (5.46) в (5.43), получим:

6t = -.

24 (б + £)

(5.47)

ИнтегрировгЛие ведется по всей поверхности подшипника s: -lsSS S+l; О ф s: 2я. Поступая и дальше по аналогии с п. 23, мы могли бы построить эквивалентную структурную схему цепи с обратной связью, найти передаточную функцию разомкнутой цепи Go (s, i) и исследовать динамические процессы в рамках асимтотической модели частотными методами. Так же, как и в предыдущем случае, частотные характеристики модели допускают ♦ уточнение методом гармонического баланса.

Ограничимся здесь выводом условия устойчивости. Условие устойчивости можно получить непосредственно из (5.44) и (5.45), для чего достаточно вычислить значение передаточной функции замкнутой цепи Go (s, i) при s = IXo и потребовать, чтобы это значение не превосходило -1.

Из (5.44) легко вывести выражение для эквивалентной передаточной функции разомкнутой цепи Go (s, О, которая будет иметь вид:

Go (s, О =

Gi (s, i)

PaRL 41

PaRL 2xo

где Gi (s, i) определяется в рамках асимптотической модели формулой (5.45). Полагая в (5.45) s = iXo- что соответствует частоте полускоростного вихря, получим а, = Gi (IXo- О- Полагая затем S = IXo в (5.42) и учитывая (5.47), на основании вышесказанного выведем условие устойчивости

где Ко = (s/oy а а, определено в (5.47). Запишем формулу (5.48) иначе:

-J--I0

PaRL

<

2 (б + £)

а, =

(5.49)

Тогда коэффициент а будет выражаться так:

Re {Хр}

d(f dt,.

Неравенство (5.49) выражает второе необходимое условие устойчивости, дополнительное к условию (5.39). Для устойчивости ротора в равновесном режиме должны выполняться оба условия. Не останавливаясь на следствиях, которые-вытекают из представленных условий (обсуждение этих условий можно найти в цитируемой выше литературе) отметим что основную роль здесь играет величина а, характеризующая вихревую жесткость подшипников. Примеры вычисления вихревой жесткостр приводятся в гл. VI.

25. Влияние на устойчивость податливости крепления машины (гиркопа)

В работе Марша [54, т. 86] отмечалось, что дополнительные степени свободы, обусловленные нежесткостью крепления подшипников, могут оказывать сильное влияние на устойчивость. Попытаемся выяснить этот вопрос в рамках асимптотической модели в 1-м приближении. Для этого возьмем снова машину с обращенным ротором, которая рассматривалась в п. 23, но расположим ось фигуры ротора вертикально (рис. 29).

Представим себе, что статор машины упруго закреплен в кардановом кольце с помощью растяжек с я с (рис. 29). Получается модель гироскопа с эластичным креплением кожуха в Кардановом подвесе.

Рассмотрим малые поступательные колебания ротора и статора машины в экваториальной плоскости без учета угловых перемещений. Колебания такой системы можно описать двумя дифференциальными уравнениями следующего вида:

М {Ае\ + Аею) = АРi -Ь Af i,;

Аёю + с Абц, = - АР 1, 9* . 131

(5.50)

где М - масса pofopa; Afj-масса сТатора; Ai = Ае + + ieAeio = Aeoj + iAe - комплексные смещения ротора и статора соответственно; с - жесткость крепления.

Силами сопротивления движению статора мы пренебрегаем и предполагаем, что крепление имеет одинаковую жесткость при смещении в экваториальной плоскости в любом направлении.

После преобразования по Лапласу с учетом нулевых начальных условий уравнения перепишутся так: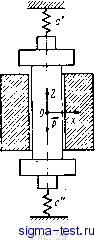

PaRL. 4xg

PaRL

(5.51)

Здесь Asio = Aeio/(6 + E); остальные обозначения даны в п. 23. В сокращенных обозначениях эти уравнения можно переписать:

Q2 - .

0 (A8i + A8io) = - G A8i -j- /13;

l-:S + Tlj A8io = G A81,

(5.51)

где Ло - , с (6 + £)

Ml (6 + £) .

Исключая из уравнения (5.51) Ae и пользуясь опять представлением эквивалентной системц с обратной связью, найдем эквивалентную передаточную функцию разомкнутого контура, соответствующего случаю нежесткого крепления.

G (s, О G(s, О

(5.52)

- Хо ;

где G (s, i) определяется выражением (5.36). В случае жесткого крепления передаточная функция G (s, i) получается из G* (s, i) предельным переходом +оо. Это значит, что при достаточно большой жесткости подвеса амплитудно-фазовые частотные характеристики Go (ш, О и Go (ш, О = lim gI (tco, i) будут про-

ходить близко друг от друга.

Зная, что устойчивость определяется положением точки К пересечения частотной характеристики с вещественной осью, посмотрим в какую сторону перемещается эта точка, когда коэффициент жесткости 7i уменьшается (рис. 28, а). Из (5.52), пола-132

гая S = получаем для этой точки Gl {i%o, i) = -

, - (5.53)

Yi - >i

Отсюда видно, что при достаточно большой, но конечной жесткости, когда у1 -XiQ > О, уменьшение жесткости приводит к уменьшению запаса устойчивости.

Влияние податливости крепления на устойчивость может быть значительным, это обстоятельство необходимо учитывать при конструировании машин (гироскопов), особенно в тех случаях, когда по техническим условиям предусматривается амортизация.

Интересно, что при малых значениях жесткости подвеса или достаточно больших угловых скоростях, когда yi -iQ < О, запас устойчивости может быть положительным.

Амплитудно-фазовая частотная характеристика при этом претерпевает качественное изменение. Отметим, что существенное значение имеет демпфирование поступательных колебаний машин.

Все эти вопросы можно исследовать с помощью асимптотической передаточной функции и уточнить методом гармонического баланса, но мы их оставим в стороне, так как они выходят за рамки данной работы.

26. Уточнение динамических характеристик методом гармонического баланса

Из изложенного в предыдущих параграфах следует, что важнейшей динамической характеристикой газодинамических подшипников является вихревая жесткость. Мерой вихревой жесткости является величина а, которая в первом приближении определяется интегралом в условии (5.39). Количественная оценка вихревой жесткости, сделанная на основании решения краевой задачи в 1-м приближении, может быть уточнена в рамках обобщенного метода РЯ-линеаризации путем вычисления аддитивной поправки. Вихревую жесткость можно найти и непосредственно из уравнения Рейнольдса путем применения метода гармонического баланса.

Рассмотрим машину (гироскоп), уравновешенный ротор которой вращается в- цилиндрических газодинамических подшипниках с произвольным профилем. Предположим, что ротор не испытывает радиальных нагрузок и вращается с постоянной угловой скоростью Q вокруг оси фигуры, совпадающей с осью подшипника. Как мы уже знаем, это положение динамического равновесия при определенных условиях может оказаться неустойчивым. Найдём эти условия.

Для этого представим себе более общий случай орбитального движения центра масс ротора под влиянием круговой вибрации

Основания, когда ось подшипника описывает в пространстве цилиндрическую поверхность.

Движение ротора в этом случае можно описать с помощью одного комплексного уравнения следующего вида (см. гл. И):

M(6 + £)(er4-8ro) = Fi[8i],

(5.54)

где == -Ь 1гщ -смещение оси подшипника; г, = + + 18 - смещение оси ротора относительно подшипника; F [г,] - комплексно-значная операторная функция, выражающая зависимость силы реакции подшипников от 8; обозначения параметров прежние (см. п. 21-23); штрих обозначает дифференцирование по безразмерному времени т = Q/2xo t. Движение основания зададим уравнением

8io = 8oe\ (5.55)

где 8от - комплексная амплитуда; v - безразмерная частота круговой вибрации основания.

Если положение динамического равновесия устойчиво асимптотически, то при достаточно малой величине s \ ось ротора в установившемся режиме будет совершать вокруг оси подшипника орбитальное движение, близкое по форме к круговому, с той же частотой v. Это утверждение следует из теории устойчивости [36 ] и подтверждается опытом. Следовательно, установившееся движение оси ротора можно представить рядом Фурье в комплексной форме

61= S , (5.56)

k- - оо

Для того чтобы найти это решение, можно применить известный метод гармонического баланса; подставить ряд (5.56) в уравнение (5.54), разложить в ряд Фурье правую часть уравнения (5.54) и т. д. Аналогично тому, как это часто делается на практике, ограничимся лишь одной гармоникой, предполагая, что высшие гармоники малы и их можно отбросить

8, = eievt. (5.57)

В правой части (5.54), также удержим лишь правую гармонику

2я V

(5.58)

Подставляя (5.55)-(5.58) в (5.54) и отождествляя коэффициенты, получим приближенное уравнение для г,:

2я V

- Л1 (б + £) v2 (е + 8oJ = I F, [г,e- ]e-vt. dx,. (5.59)

В этом уравнении неизвестная 8j является комплексной амплитудой. Можно, однако, задатьгтак, чтобыs, было вещественно.

Предположим, что это условие выполнено, и обозначим г, = = р. Перепишем уравнение в следующем виде:

Л1 (б + £) v2p + {-\ F, [ре-. ] e-vx, dx, =

(5.59)

Это уравнение дает возможность определить радиус р средней орбиты установившегося вихревого движения оси ротора и arg 8о при заданных v, 8om и прочих параметрах. Следует помнить, что искомый режим реализуется лишь при выполнении дополнительных условий устойчивости, которые не следуют из (5.59). Если мы из (5.59) перейдем к пределу при \ so\-0, то получим уравнение свободных незатухающих колебаний, которые возможны лишь на пороге устойчивости, при этом частота свободных колебаний должна удовлетворять уравнению

-у F, [ре- ] е-- dx, = 0. (5.60)

Так как первый член вещественный, то из (5.60) получаем следующие условия:

2я V

(6f £)v + -lim ( ReiF,[pe-4e--}di = 0;

2Я V

lm{F,[pe]e-}dx, = 0.

(5.61)

Разделив все члены первого уравнения на PaRE представим его в виде

М (б + £)

PaRL

1Ш 7г-

vPaRL 2я J

-i- Re [ре- ] е-} dx, = 0.

(5.62)

Сравнивая это уравнение с условием (5.39), найдем, что второй член выражает вихревую жесткость подшипника с обратным знаком (см. п. 23).