8. ДВИЖЕНИЕ СО СВЕРХСВЕТОВОЙ СКОРОСТЬЮ

Проблема движения тел со сверхсветовой скоростью - тахионов так и остается нерешенной проблемой, несмотря на тысячи статей, которые ей были посвящены [4, 100]. Иногда такие движения наблюдаются в астрофизике, хотя их достоверность все же не окончательная и вызывает сомнение [32]. Тем не менее поиск сверхсветовых обобщений СТО вполне оправдан, так как позволяет полнее представить СТО. Нас будут интересовать эффект Доплера при сверхсветовом движении и соответствующее изменение масштабов времени и координат.

Эффект Доплера позволяет рассмотреть движение излучателя и приемника со сверхсветовыми скоростями. Хотя проблема сверхсветовых частиц - тахионов пока еще не решена, однако движения со скоростями больше скорости звука подробно изучены. Для них используется преобразование Лоренца для v > 1 [4, 76, 100]. Само сложение сверхсветовых (сверхзвуковых) скоростей согласно (2.9) и (2.30) дает < 1, т. е. досветовую скорость. Если в (2.9) Vi = -v, причем > 1, то в (2.5) х -> -> -X, г -> -t. Это означает, что порядок событий во времени изменяется на противоположный. В процессах с участием сверхзвуковых (сверхсветовых) тел от скорости зависит не только длительность сигнала, но и сам порядок событий. Даже бывает так, что следствие и причина могут поменяться местами. Поэтому, хотя сигнал и испытывает доплеровский сдвиг частот, однако может в ряде случаев поступать на приемник в обратном порядке тогда, когда излучатель приближается со сверхсветовой скоростью. Однако это не мешает подсчитывать излученные и принятые импульсы и, воспользовавшись эффектом Доплера, исследовать масштаб времени согласно соотношению vt = N, Рассмотрим примеры.

Пусть В излучает сигнал частотой Vq и удаляется от А со скоростью и>1(и>с, с=1). Тогда В в течение какого-то времени будет сначала принимать низкочастотный сигнал = ioViP - + О- Затем, если В возвращается к Л со сверхсветовой скоростью, в течение времени прием-

ник А будет принимать высокочастотный сигнал Vx ~ oV- в обратном

V - 1

порядке (см. диаграмму на рис. УП1.5). Точка а на оси обозначает момент прилета тела В в точку О (где расположен приемник А). Если В двигалось со сверхсветовой скоростью v > 1, то после возвращения В к А все еще будет поступать сигнал низкой частоты, излученный В во время удаления. Он будет поступать и во время приближения В к А. После прилета В будут поступать к А и сигналы высокой частоты в обратном порядке (см. рис. VIII.5), которые в точке 3 смыкаются с сигналами низкой частоты. Спрашивается, какое время Т пройдет по часам А от момента отлета тела В до его возвращения? Из рисунка видно, что

T=t-t-A- (8-0

Для г, г5 и имеем соотношения

pjjc, Vin.5 Обмен сигналом между А и В Скорость сближения А и В больше скорости света

Откуда (см. (29.а))

+ 1)

(и-1)

(-1) (у + 1)

]=2Гв(-1) / =

(8.3)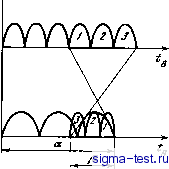

Раньше при v < 1 мы имели = б(1 - v)~\ т. е. > t. Если v -> 1 - О, то Теперь, при и > 1> имеем > ty когда v - I < I.

Для интервала > 2 < ; в пределе v получим -> 0.

Пусть тело В улетает, а затем возвращается к Л со сверхсветовой скоростью > 1. При этом а излучает сигнал частоты vq, распространяющийся со скоростью света с = 1. Понятно, что если а начало излучать в момент отлета В, то сигнал с а достигает В, когда В будет на обратном пути и будет принимать только высокую частоту. Следовательно, чтобы В принимало сигнал от а все время, необходимо, чтобы а начало излучать еще до старта В за некоторое время . Всего же после начала излучения, отлета В и возвращения 5 на должно пройти время + i- Понятно, что в течение времени (В удаляется) приемник В будет принимать низкую частоту, а затем в течение времени Та - высокую. Совершенно аналогичный пример мы рассмотрели для зеркала Z в разд. 6. Имеем

аоГвх. (л+?)o=i. (8.4)

Интервалы времени движения В по часам В при прохождении в прямом и обратном направлениях одного и того же пути с одной и той же скоростью равны tB = tQ= Шв Откуда

= tl(v-ir\ (8.5)

Мы пришли снова к соотношению (3.3).

Теперь можно рассмотреть движение с разными скоростями. Пусть, например, излучает а, а В улетает с досветовой скоростью v(v < I) п прилетает со сверхсветовой m(w > 1), Имеем

tAVotvivl Г>о=/;( ). (8,6)

Мы не знаем пока, сколько времени В потратило на обратный путь, но можем положить г = уГв* Тогда

tA = + = г (1 + ур (V(l - v)/(\ + и) + 7 V( + l)/( - О). (8.7)

Пусть теперь В проделает тот же самый путь, однако излучает сигнал Д

а принимает А. Тогда

4о = >Ли), tVo = tvUu). (8.8)

Причем снова после прибытия В через время Т (прошедшее после отлета) на приемник А все еще будут поступать как низкочастотный сигнал в прямом порядке, т. е, так, как он бьш излзен, так и высокочастотный сигнал в обратном порядке. Поэтому

T=tA-l . (8,9)

Время Тв, которое тело В потратило на обратный путь, двигаясь со скоростью W, связано со временем Тв. в-Ув- Откуда

Т=А-А=1( + -v)-yy/(u- Щи + 1)]. (8.10)

Приравнивая (1.7) и (1.9), находим

V /и - 1 = -V--г,

и 1 -

Есть большое сходство (8.11) с (6,6). Это означает, что лоренцево сокращение расстояния наблюдается и в сверхсветовой области движений. Функция

л W + У

u\/l -v - 1

обладает следующими свойствами: /(ц, 1) = \/(и + 1)/(и - 1) /(1, v) =

= v(i + i)/(i-i); /(-,У) = (и + Vi=n7)-

Можно рассмотреть еще целый ряд задач для движения тел со сверхсветовыми скоростями, например, изменяющимися на всем цикле движения. Конечно, хотя формула сложения двух сверхсветовых скоростей и дает суммарную досветовую скорость (так же как сумма двух досвето-вых), однако эффект Доплера дает более полное представление о непосредственно наблюдаемых явлениях. Еще точнее эти явления можно рассмотреть, комбинируя эффект Доплера с временем прихода сигнала в каждом конкретном случае. Это обстоятельство позволяет более подробно исследовать эффект Доштера и времена прихода сигналов для волновых процессов разной физической природы. Например, если I > v > Л, то, полагая и = vlyjlv - 1 > 1, имеем у = \. Это означает, что время движения тела с досветовой скоростью v{v > Vi) и со сверхсветовой скоростью и по одному и тому же пути будет одним и тем же в каждой из движущихся инерциальных систем координат. Такое возможно только в теории относительности благодаря лоренцеву сокращению расстояний. Поэтому тахионы и брадионы ( быстрые и медленные частицы), для которых скорости и и w находятся в соотношении

у-2 +vv-=2, (8.14)

различать и обнаружить по времени пролета (по внутренним часам) од-