gopTOxpOHHOe преобразование Лоренца оказывается эквивалентным одному собственному преобразованию с некоторой скоростью и вращению системы координат. Пользуясь результатами работы [101], можно отделить суммарное вращение от скорости ¥(11;! < 1). Однако эти вопросы не связаны с эффектом Доплера, который рассматривается в данной главе.

Рассмотрим эффект Доплера в движ)ацейся среде. Пусть тело движется со скоростью v(x = vt) в покоящейся среде с показателем преломления : ci =с/п, п> I, Электромагнитная или световая волна в такой покоящейся среде имеет вид f(t - x/ci). Пусть волна представляет собой некоторое число импульсов следующих с частотой и: N = u(t -x/ci). Тогда, переходя к системе координат, движущейся со скоростью и, имеем

t = (1 - v/cr (t - vx/c), x = (1 - vVcy\x -vt), (3.36)

Понятно, что N - инвариант, т.е. число импульсов в любой системе координат будет одно и то же. Следовательно,

N=v(t-xlci) =u\t-х1с[) (3.37)

iit-xfci) = (v/y/l -vVc)[tvt/c[ - vx/c -x/cl (3.38)

где v\ c[ - частота и скорость волны в системе координат, движущейся со скоростью V.

Рассмотрим цепочку волн (3.33) в один и тот же момент времени Г = 0. Тогда, полагая в (3.3) Г = О, имеем

Теперь рассмотрим ту же цепочку волн, проходящих через сечение х = 0. Полагая в (3.3) х = О, находим

Из (3.34) и (3.35) получаем

Vi-v ,- -fill- с; = -1 (3.41)

I+U/Ci l+UcJ/Ci \-VCilC2

Таким образом, скорость с[ увлечения света движущейся средой при движении света по течению (+) и против (-) будет

Ci±v c/n±v

cl = --г =-, (3.42)

\±vcjc l±v/cn

a доплеровское изменение частоты

К= , / (3.43

Знаки в (3.38) надо брать в соответствии с тем, чтопри движении света по направлению вектора v частота уменьшается, а скорость с+ увеличивается: с > ci, и наоборот. Если в движущемся со скоростью v потоке имеется зеркало, которое движется со скоростью Ui, то отражение света от него можно рассматривать как бы в анизотропной среде со скоростями с+ ис соответственно. Эти скорости можно использовать в решении (3.21) для определения соответствующих доплеровских смещений частот [18, 73].

4. КИНЕМАТИКА ДВИЖУЩИХСЯ ТЕЛ НА ОСНОВЕ РЕЛЯТИВИСТСКОГО ЭФФЕКТА ДОПЛЕРА

Рассмотрим снова, как и в разд. 2, два гела Л и В. Одно из них будет излучать электромагнитную (световую) волну, а другое - принимать. Одно будет неподвижным, а другое - двигаться прямолинейно по замкнутому циклу, то удаляясь со скоростью и, то приближаясь к исходному месту, где Л и j5 совмещены.

1. Пусть тело А - приемник - покоится, а тело В излучает частоту Vq, удаляясь от А со скоростью v < I (и < с), а затем приближается снова с такой же скоростью. Имеем

Уравнения (4.1) совершенно идентичны с (1.11) и (1.12), только Uy, и Vx - релятивистское доплеровское изменение частот согласно (2.11). В соответствии (1.13), используя (2.12), получаем

tl=t t = ts (volVxVoK) = 1(1 -v)-\ (4.2)

Мы получили формулу замедления времени. Согласно ей время на движущемся теле В течет замедленнее (tg< rj), чем на неподвижном А.

Такое замедление произошло благодаря релятивистским формулам эффекта Доплера при световой связи между А п В. Конечно, реальной связи между АиВ может и не быть. Это просто прием, позволяющий контролировать течение времени нгА и В.

2. Рассмотрим тот же цикл движения тела В тогда, когда А излучает частоту 10- Тело В вначале удаляется от Л в течение времени tg, принимая низкую частоту Затем в течение такого же времени Tq тело В приближается, принимая уже высокую частоту Vx- Приравниваем количество импульсов как испущенных, так и принятых с той или иной частотой; причем на пути от А частота низкая, а на пути к А частота высокая. Имеем два уравнения

do=r., tPvo=tsux, (4.3)

Эти уравнеш1я полностью аналогичны (1.14). Откуда, используя (2.12), находим

fA=4tP =2tB(l-v)-=ti(l ~vr\ (4.4)

Мы снова получили формулу замедления времени. Согласно ей космонавт, улетевший на ракете, вернется на Землю более молодым, чем его близнец, оставшийся на Земле (парадокс близнецов) [18, 19, 39, 94, 99, 100].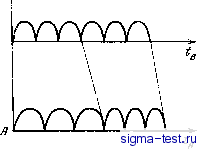

рис. VIIi.3. Оьмен сигналом между А иЗ

Приведем еще один вьюод форму- лы (4.2) и (4.4), связьюающие и t. Пусть снова В движется и излучает сигнал. Обозначим время, определенное по часам А, в течение которого тело В удаляется. Понятно, что А будет принимать низкочастотный сигнал несколько дольше, а именно

+ АГ4. Тело В уже повернет обрат-но к л, а низкая частота все еще будет

идти некоторое время Дг =а/с = а (при с = 1). Так как Г4 = a/v, то Лг = = vtA- Аналогично находим, что сигнал высокой доплеровской частоты, излучаемый В при приближении к А, будет приниматься в А уже не время /4, а меньшее время - Д. Это происходит потому, что сигнал высокой частоты еще должен дойти до Л, преодолевая расстояние а. Приравнивая число излученных и принятых импульсов, имеем для fj = 2

= tA K(l v)vA- V)] -2tAVo{l - V) -/r>o(l - vr\ (4.5)

Bo всех случаях получилось одно и то же релятивистское соотношение для времени, текущем на покоящемся теле А и движущемся В, Из него следует, что стареет быстрее покоящееся тело, поскольку fj> rj.

Процесс изменения масштаба времени можно изобразить на простой диаграмме (рис. УП1.3). Вдоль горизонтальных осей отложено время, протекающее на Л и на В, На тех же осях изображен один и тот же периодический процесс, когда В излучает (вариант 2), сначала удаляясь от А, а затем приближаясь. А принимает те же самые импульсы с низкой частотой какое-то время t{t h)- Затем А принимает импульсы с высокой частотой. В результате суммарное время = будет больше, чем 2 tB. Это видно на рис. Vni.3.

Если, кроме импульсов с частотой Pq, которыми обмениваются тела Л и В, ввести HdL А и В еще один совершенно идентичный периодический Процесс с частотой До (идентичные часы , идущие на Л и 5), то его можно сопоставить с непрерывно текущим временем, описываемым параметром t Если внутри крупного импульса частоты Vq укладывается п мелких импульсов частоты До, то в импульсах уложится nN = Ов мелких. Поскольку обмен излучением между А и В происходит крупными импульсами, то они сначала растянутся (В удаляется), а затем сожмутся, так что в сумме дадут интервал а+ 13, больший, чем ао + j3o (рис. УП1.3).

Если точно такие же часы т.е. с частотой До имеются на покоящемся теле А, то они сделают больше колебаний маятника, чем аналогичные часы на i5:

(nN) = (nNB)(i-v)

(4.6)