этого, используя МКР и двигаясь в направлении источника (источников), можно по волновой голограмме - поле на нормальном сеточном волноводе - восстановить поле во всем волноводе.

Вопрос о выделении углов прихода лучей и времен прихода на фоне шума давно обсуждается в литературе [8], Однако если первая часть задачи - выделение углов и времен прихода - решается довольно успешно, то вторая часть - о восстановлении поля - решается, как правило, тоже в лучевом приближении. При голографическом рассмотрении на первом этапе лучи использовались для восстановления поля в нормальном сечении. Затем обращение фронта можно было выполнить на основе МКР в волновом приближении.

Если же волновод заполнен слоистой средой, то волны (лучи) испытывают в нем фокусировку. Такой волновод работает как линза с фокусным расстоянием 25 км [84]. Понятно, что в нем фронты волн искривляются, хотя и очень незначительно. Все же если по-прежнему на некотором небольшом апертурном сеточномготрезке мы вьщеляем углы прихода лучей и их относительные времена прихода путем соответствующей обработки (конечно, на фоне шума), то каждому лучу в пределах размеров апертурного отрезка можно сопоставить некоторую плоскую волну. Суммируя эти волны, можно получить поле на апертуре заданной длины. При этом кривизна волнового фронта может еще не сказаться.

Однако, если кривизна фронта мала, а фокусное расстояние в слоисто-неоднородном волноводе велико, можно, как и выше, рассмотреть группу плоских волн, соответствуюпщх вьщеленным углам. Их можно продолжить и вне заданной апертуры на некоторое расстояние. Тогда ошибка в фазе каждой волны из-за слабой кривизны фронта еще не накопится сильно. Апертурный отрезок и поле на нем можно будет продолжить вверх и вниз в волноводе. Конечно, расстояние, за которое можно выйти из реальной апертуры, на которой измеряются углы прихода волн, будет зависеть от частоты и от других параметров задачи. На низких частотах это расстояние можно считать большим, чем на высоких.

Затем, выйдя за апертуру малой величины и воспроизведя поле на голограмме в виде апертуры большой величины, можно снова обратиться к МКР и реализовать полную волновую картину вне продолжений голограммы. МКР позволяет это сделать быстро и надежно. Он позволит рассмотреть различные величины продолженной апертуры, исследовать частотное наложение полей (см. разд. 10, гл.1). Так лучевая обработка может успешно быть совмещена с волновой голографической обработкой. Преимущества такого комбинированного пути очевидны и вполне реализуемы как в численных модельных экспериментах, так и в реальной ситуации, когда измеряются углы прихода лучей (волн) и относительные времена их запаздьюания (фазы).

Совокупность точек, в которых фаза колеблется в один и тот же момент времени одинаково, называется волновым фронтом. Точность измерения волнового фронта зависит от длины волны и, как правило, имеет величину 0,05-0,1 [87]. *Если радиус фронта волны R, допустимая ошибка в измерении фазы (в единицах длины б > О, то имеем (R - бУ + = R,2h - размеры апертурного отрезка по вертикали. Например, при Л = 25 км, 5 = 1 м имеем 2h с- 450 м; при 5 = 0,2, 2Л = 200 м.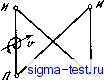

8. ТОМОГРАФИЯ В ВОЛНОВОДЕ НА ОСНОВЕ ВОЛНОВЫХ ПРЕДСТАВЛЕНИЙ

Пусть в трехмерном слоистом волноводе на некоторой глубине расположен точечный гармонический излучатель. На расстоянии R от него расположена вертикальная цепочка гидрофонов (сеточный отрезок), принимающих амплитуду и фазу гармонического сигнала. Тогда, зная свойства волновода и используя МКР для обращения фронта поля, заданного на вертикальной антенне, можно восстановить поле в волноводе и получить пик, выброс в точке, где находится излучатель. На трассе излучатель-приемник среда может изменить свои свойства, например, благодаря прохождению через трассу вихря, циклона или антициклона, внутренних волн и других образований. Измеряя поле на вертикальной антенне и обращая фронт, пик в точке, где расположен излучатель, получить уже не удастся.

Рис. VII.5. Прохождение вихря через прямоугольную область

И - источники, П - приемники

Если В вершинах прямоугольника расположить два локализованных излучателя, а в других двух вершинах - вертикальные сеточные антенны, то трасс будет уже четыре (рис. VII.5). Пусть вихрь движется прямолинейно со скоростью V по прямой у = ах b и пересекает трассы в моменты времени Го, hy h- Тогда нам известны величины Tj = (tf - tj i)j= 1, 2, 3, а величины а и b неизвестны. Имеем следующие расстояния Гь Г2, Гз между точками пересечения трасс вихрем:

П = y/iyj-yj-if (xj-Xj-lf= (Xj - xi 1 )Vl a\ /=1,2,3. (8.1)

Откуда

r, +Г2+Гз=<2\/Т+7, (8.2)

где Q - длина стороны прямоугольника между двумя вершинами, которые также известны. Имеем

Тх =riu, Г2=Г2и, Гз=гзи. (8.3)

Следовательно, зная v и зная Г2, Г3, можно найти rj, 2 и Г3. Тогда из формулы (8.2) можно определить параметр а, характеризующий угол наклона траектории вихря, проходящего в прямоугольнике, к его сторонам. Можно определить и другие параметры задачи.

Таким образом, использование МКР при нарушении свойств трассы между приемной и излучающей системой позволяет, во-первых, фиксировать это нарушение по распльюанию пика в точке локализованного излучателя. Во-вторых, при более детализированном рассмотрении, используя ряд трасс, свойства вихря можно изучить томографическими методами.

9. РЕШЕНИЕ РАЗНОСТНОЙ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ МЕТОДОМ КРАЕВОЙ ЗАДАЧИ

При вычислении волновых полей в слоисто-неоднородных средах широко применяется метод нормальных волн. При обработке информации, измеренной на сеточном отрезке, т.е. на антенне, состоящей из эквидистантно расположенных гидрофонов, также необходимы основные характеристики нормальных волн. Для нахождения нормальных волн необходимо численно решить задачу ПШ.

Задача ШЛ состоит в нахождении собственных значений Л и собственных функций Un уравнения

иЬ) = к(у)и(у) = Хм (у), и(0) = и(7г) = 0. (9.1)

На ЭВМ краевую задачу ШЛ решают часто методом начальной задачи, полагая и(0) = О, и(0) = а. Известно, что такой путь связан с рядом трудностей. Например, при разностной аппроксимации уравнения (9.1) в тех областях интервала (О, я) на оси у, где коэффициент к(у) - X отрицателен и имеет большую величину, решение начальной задачи может экспоненциально расти. Поэтому трудности вьиисления Л и uiy) методом начальной задачи особенно увеличиваются с ростом частоты, когда вещественный коэффициент к (у) растет. В то же время решение краевой задачи для сред с потерями, когда к(у) ~ комплексная функщ1я, не встречает принципиальных трудностей. В таких средах нет резонансных явлений, а метод решения разностного аналога краевой задачи - метод прогонки - устойчив в широких пределах.

Поэтому вместо (9.1) рассмотрим следующую задачу. Введем малые потери и воспользуемся приближенным методом решения задачи ШЛ. Имеем следующее уравнение и условия на границах:

v*(y) + (О) + i)v(y) = Ф) КО) = О, v(n) = 5. (9.2)

Вычисления проводим для вещественных значений параметра X на полуоси X < max к(у) с таким шагом, чтобы обнаружить максимум функции

m(X)=}\v(X2y)\dy. (9.3)

Причем

Im }vb)v(y) + ((у) - X + id)v(y)v(y) =

= lmvb)v(y)\lJ8\v\\ldy. (9.4)

Следовательно,

/I v\ dy = -Imvin). (9.5)

Это соотношение позволяет избежать интегрирования (т.е. суммирования для разностной задачи) в (9.3). При переходе к разностному аналогу (9.2) используем метод прогонки. В этом и состоит путь решения задачи ШЛ методом краевой задачи.

В качестве примера рассмотрим случай к = const. Тогда решение (9.2)