J.2ff

- 0,SZ8S-

o,om-ff,jffj-

0,3JfU-

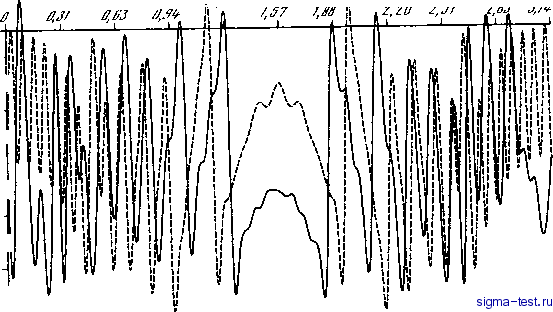/ --Z

Рис. Vn.3. Сравнение фаз поля

; - фаза восстановленная по амплитуде; 2 - фаза, взятая из вьиисленного поля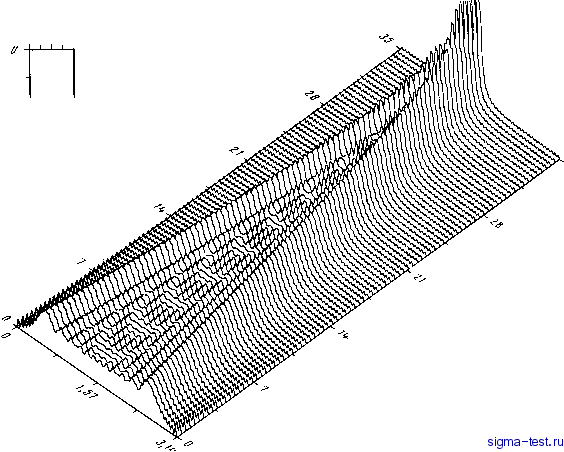

Рис. VII.4. Поле распределенного источника в волноводе с восстановленной фазой

сейчас открылась возможность получать неверное решение задач аж с точностью до 15 знака !

Однако МНВ, хотя он и неприменим непосредственно к неслоистым волноводам и к полям волн, испьп:ьшающих взаимную трансформацию и идущих в двух различных направлениях, может быть критерием как для контроля неслоистости волновода, так и для контроля однонаправленности волн в нем. В этом несомненно еще одна из привлекательных сторон МНВ, на которой следует остановиться. Эта сторона важна именно в алгоритмическом аспекте, так как неизбежные ошибки при измерениях и вычислениях поля всегда существуют даже в слоистом волноводе [45].

После того как поле вычислено каким-нибудь методом, например сеточным на основе ПУ, или ПУГ, или измерено в процессе эксперимента, возникает проблема, как представить уже найденное поле в виде суммы нормальных волн в том случае, если волновод регулярный. При этом следует рассмотреть путь, при котором нет необходимости решать задачу ШЛ, раскладывать функцию, характеризующую источник по собственным функциям волновода, а затем сопоставлять известное поле и поле, найденное методом суммирования нормальных волн. При таком сравнении всегда могут быть ошибки, так как в МНВ суммирование просто обрывается на некоторой нормальной волне, а в МКР никаких суммирований вообще нет, так как решается само исходное уравнение. Зная поле в достаточно большой области волновода, решение задачи ШЛ можно выполнить иначе.

Пусть и(х, у) = Х апФп(у)ехр(1х) - поле в регулярном волноводе,

без потерь, измеренное или вычисленное в результате каких-то процедур. Нам известна только функция у), а величины д , / (у), неизвестны. Чтобы их найти, рассмотрим следующий алгоритмический процесс. Вначале образуем такую функцию от параметра t:

F(0=/ aexp(ix-ixt-p\x\)dx, (5.1)

где ±А - пределы интеграла (суммирование); , t, р - некоторые параметры. Вместо F{t) можно взять функцию

Fi (О = / aexp(ix - ixt - px)dx. (5.2)

Для дальнейшего это несущественно, так как пределы ±Л мы выбираем достаточно большими, чтобы подынтегральное выражение было малым. Для вывода теоретических формул можно считать, что Л >. Тогда из (5.1) приближенно при А-° находим

F{t)=2apl\p {k-tf], (5.3)

Если О <р < 1, то F(t) имеем максимум F(/o) = lajp при fo = а затем быстро убывает. Следовательно, вычисляя функцию

Число узлов по вертикали определяет число линейно-независимых собственных функций сеточного волновода, а характеристика направленности источника отбирает из этих функций некоторое количество с вещественными коэффициентами -амплитудами возбуждения. 162