-а <у <а, но пт всей оси при - > <у <7Г. При этом выделим значение интервала -а < у < а, так что введем некоторый быстро убывающий вне интервала весовой множитель ехр {-у/а). Полагаем

iU=o = exp(/V/2R)exp(-/y). (2.3а)

Для уравнения 2ik + Vyy = О легко находим решение начальной задачи с условием (2.3а) в виде простой формулы

V(x,y) = [1 +2Ьс/(А:/)]-/ехр((- уУЬ)[\2ix/(kb) Г ), (2.4)

где l/b = +/V(2). Следовательно

I 1 + 2ix/(kb) I =(1 -x/Rf +4xV(fl). (2.4а)

Выражение (2.4а) имеет минимум при Xq = R[l + ARKka )] ~\ Область R < Угак соответствует зоне Френеля. В ней приближенно х - R. Соответственно модуль решения (2.4) имеет максимум при л: - R.

Когда источник расположен в зоне Френеля на оси х (при = 0), тогда его местоположение несложно найти. Это можно сделать по максимуму волнового поля, найденного перед отрезком -а<у<а, В более общем случае необходимо по максимуму поля определить не только расстояние, но и направление (угол </?) на источник, который расположен в некоторой

точке Хо, Зо =0 + .Vo;.Vo = psint/?. Тогда аналогично формуле (2.2а), считая р большим, имеем при л: = О .

exp[/V(-o) +0-.Vo)]=o exp[P->A:/(2p) + :xVo/p].(2.5)

Кроме того, по-прежнему предполагаем, что заданное на оси -°<.V < °° поле (2.5) умножается на весовой множитель с коэффициентом а = асощ). Однако для небольших углов когда справедливо приближение ПУ cos(/?~l, полагаем2 - а.

Решение ПУ 2ik\)y + и-;- = О ищем в виде

{х, у) = 7 Щ) exp(/v x)dl (2.6)

2ik

Тогда

Следовательно,

1 -ОС / у2 iky \

F() = - / 1-- --- iky sinp - iivdy. 27Г -оо \ /7 2о

(2.7)

2п -оо \ д2 2р Воспользовавшись табличным интегралом

/ exp(-pv ±qy)dy = \/п/рe\p(q/4р), (2.8)

+ 00

находим F() =-=ехр(/4р);р = Ila,q = i(ksinip - ?). Затем, еще раз 2\1пр

Используя формулу (2.8), находим согласно (2.6) и само решение снова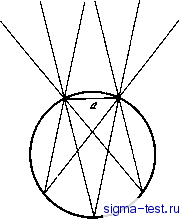

Рис. Vn.l. Равноугловые области перед отрезком д

в виде простой формулы (2,8), в которой 1

ik + 2аX

а X

Pi = - + - = -;-

4 2ik 4аЧк

;а9)

Поиски максимума модуля v(x, у) \ лучше всего начать с поиска его максимума по X при у = 0. Тогда в окрестности х=Хо, где находится максимум, находится и источник, т.е. для небольших углов он находится вблизи линии X = Xq, Чтобы ползить всплеск , максимум поля, совсем необязательно упереться в источник: достаточно пройти где-то рядом с ним. Таков первый этап приближенного поиска максимума и координат источника. Затем на втором этапе, передвигаясь по линии х =Хо вдоль оси, находим максимум модуля поля на этой оси в точке у =Уо- Используя выражение (2.9), нетрудно убедиться, что величина у = уо соответствует углу

Тем самым найдены направление на источник волнового поля и расстояние до него, если он расположен в зоне Френеля.

Конечно, источников может быть несколько. Тогда и максимумов I v(x, у) I также будет несколько. В некоторых случаях они будут сливаться, а в некоторых их удастся различить. Вне зоны Френеля максимумы будут отсутствовать. Однако направление на источник и в этом случае можно определить обычным образом, анализируя угловой спектр.

Параболическое уравнение дает правильный результат в случае, когда источник расположен под небольшим углом к оси 3;. Если же перед некоторым отрезком -а <у <7i имеется область в виде угла большого раствора -фо < ф < фо, то, конечно, непосредственно использовать ПУ нельзя. Однако эту область можно разделить на ряд подобластей с углами малого раствора -ф < Ф < Ф (Ф < Фо/), в каждой подобласти ввести свои координаты х, у, причем - асо$ф. Такие области будут заполнять большой угол и частично накладываться друг на друга внутри него (см. рис. vn.l). Но это не существенно: источники, обнаруженные в одной из областей малого угла раствора, могут быть обнаружены и в другой, а затем идентифицированы. Сам же угловой спектр поля, приходящего на апертурный отрезок -а<у<а просто получается путем вырезания соответствующей полосы углового спектра всего поля, представленного интегралом Фурье по углам. Ясно, что при таком разбиении зона Френеля будет уменьшаться в зависимости от угловой направленности на источник. Самой протяженной зона Френеля будет в направлении, перпендику-

лярном апертурному отрезку. Под скользящими углами она будет мала, как это и должно быть.

Если на апертурном отрезке заданы просто числовые значения поля /О) то аналитическими решениями, рассмотренными выше, не удается воспользоваться. Тогда необходимо использовать либо интегральное решение дифференциально-разностного ПУ (2.1), либо его численное решение на сетке. Вычисление интеграла (2.2) требует большого объема расчетов. Поэтому применение МКР более эффективно. Если шаг по у постоянен, то размеры угловой области, где может находиться максимум поля и сам источник, увеличиваются по мере удаления от апертурного отрезка. Чтобы ограничить число узлов в сетке и повысить эффективность программ МКР, бьшо рассмотрено проведение вычислений на цилиндре при периодическом условии для решения ПУ. Максимумы поля, соответствующие источникам, бьши обнаружены и в этом случае.

3. ОДНОМЕРНАЯ ВЫБОРКА ВОЛНОВОГО ПОЛЯ В ТРЕХМЕРНОМ ВОЛНОВОДЕ

Когда волновое число А: в УГ или ПУ известно, решение уравнений при заданных условиях на границах и заданном источнике поля представляет лишь технические трудности. Так обстоит дело с двумерными и трехмерными прямыми задачами. Однако в трехмерных обратных волноводных задачах могут встречаться случаи, когда известен только интервал, в котором заключены изменения горизонтальных волновых чисел, характеризующих распространяющиеся волноводные моды.

Действительно, гидроакустический волновод - подводный звуковой канал представляет собой пространственный фильтр распространяющихся под разными углами к его границам нормальных волн. Большая часть из них рассеивается на взволнованной поверхности и поглощается в дне в процессе распространения звука. И лишь небольшое число волн, направления которых заключены внутри угла 7 = ±5°, проходит в волноводе большие расстояния. На горизонтально расположенной ненаправленной антенне -сеточном отрезке - они все как бы складьшаются и дают суммарное поле. Отдельные моды из этого суммарного поля уже никак не выделить. Однако для малого угла 7 приближенное представление о месте локализации максимума поля вблизи источника звука получить все же можно, пользуясь слабым разбросом углового направления распространения мод по вертикали и тем, что продольные волновые числа мод близки к к.

Рассмотрим пример. Пусть

u(x,z) = S адг8ш(Аг2)ехр (/ x). (3.1)

- поле распространяющихся нормальных волн в однородном трехмерном волноводе О < Z < тг; 5 = \/ - / - направление их распространения. Пусть на своем пути волны встречают горизонтальный сеточный отрезок Z = zo (г =0), расположенный под углом к оси х: х = i?sin(/? + rcost/?. Тогда на отрезке будем иметь поле

/(т?) = 2a sin(A2>;o)exp(/ T?sin(p),