6. После вычисления поля в регулярном волноводе, используя его численные значения на сетке, можно найти продольные волновые числа и собственные функции задачи ШЛ. Эти величины проверяются путем подстановки в само уравнение ШЛ. Поле вычисляется также суммированием нормальных волн.

Остановимся на некоторых из перечисленных вопросах. Рассмотрим методы контроля на ряде примеров.

Конечно явные и неявные схемы с аппроксимацией Ух Ууу не на трех, а на пяти соседних узлах можно использовать не только для получения более точного решения. Пятиточечные схемы пригодны для контроля точности значений поля на сетке, вычисленных с помощью трехточечных схем для производных. Это трехточечное поле подставляется в пятиточечную схему. Результат при этом, естественно, отличен от нуля. Его можно перенести в правую часть дифференциального уравнения. Тогда невязка в пятиточечных схемах, т.е. правая часть уравнения, даст величину ошибки. Если же теперь снова решить это уравнение уже с правой частью (со знаком минус) аппроксимируя дифференциальные операторы трехточечной схемой, то можно уменьшить ошибку. Поясним этот универсальный метод контроля и повышения точности на простейшем примере.

Рассмотрим уравнение 3; {х) + ку (х) = О и его частное решение у (х) = = ехр {ikx). Вводя сетку с шагом h и аппроксимируя у {х) по трехточечной схеме, получим решение у{х) = ехр {гкх), где cos кИ = I - V2 Чтобы оценить, какую ошибку мы при этом допускаем, подставим полученное решение ехр (iKx) в у (х) + ку (х) = О при пятиточечной аппроксимации производной по формуле Ричардсона:

7з {[y(x + h)y(x-h)-2y(x)]/h] - (2.1)

- V3 \y(x2h)y(x-2h)-2y(x)]/4h]\ +ку(х) = Е,

Справа в (2.1) стоит невязка - искомая ошибка Е, Находим Е = k(kh)/12, Величину (khf 1\2 можно отнести в правую часть уравнения. Тогда она будет характеризовать амплитуду некоторых ложных источников , возникших вследствие разностной аппроксимации.

Можно также положить к = к{\ - Л/12), т.е. отнести величину Е к неточности задания коэффициента в исходном уравнении, например скорости звука с в этой или в более сложной волноводной задаче. Оценка раз - с дая пятиточечной схемы в случае ПУГ дает Сраз - с - 10, что соответствует точности измерений с.

Найдя Е-Е{х) (а в более сложных задачах - Е{х,у)), можно положить

f\x) + к%) = -Е (2.2)

Это позволит на следующем этапе вычислений по трехточечной простой схеме по прежней программе значительно уменьшить ошибку. Такой путь контроля точности и уменьшения ошибки является универсальным. Он годится для любого из рассмотренных в книге уравнений и для схем с любым количеством узлов. Например, можно проводить вычисления производных по пятиточечным схемам, а контроль точности осуществлять по семиточечным. Тогда оценки дают еще на два-три порядка меньшую погрешность. Получаемую при этом невязку можно отнести либо в правую часть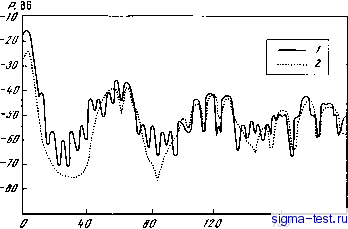

Рис. III.2. Горизонтальный разрез поля в слоистом волноводе глубиной 5 км при частоте 25 Гц

I - трехточечная ЯС, 2 - МНВ

-j0 -z0 -j0

j0 -50 -70 -60 -so

z 6 8 10 iz 75 /0 j:, км -1-1-\-1-1

п-\-1-г

Рис. 1П.З. Мелкое море (глубиной 200 м)

1 - неявная схема с усреднением, 2 - МНВ

уравнения (ложные сеточные источники поля), либо к неточности определения коэффициентов уравнения.

Приведенные методы бьши применимы для самых различных классов волновых задач, которые решаются методом сеток. Приведем примеры расчета поля точечного гармонического источника в слоисто-неоднородном акустическом волноводе для модели (рис. П1.2) глубокого океана - 37 распространяющихся нормальных волн в водном слое, на глубине 5,579 км, лежащем на жидком однородном полупространстве и для модели мелкого моря (рисЛП.З) -две распространяющиеся нормальные волны в водном слое, на глубине 200 м, с учетом жидкого поглощающего грунта. На рис. 3.2 и 3.3 представлены для сравнения кривые спадания уровня поляР в зависимости от расстояния на заданном горизонте Zp (глубина источника z о), вычисленные по явной трехточечной разностной схеме для двухслойной

модели плоского волновода - кривая 7 и по методу нормальных волн (см. рис.111.2, по программе В.Д. Крупина Zq = 253,9 м, zp - 865,5 м; рис. П1.3 -поарограмме В.В. Бородина Zq = zp = 170 м) - кривая 2. Расчеты проводились для частоты 25 Гц, соответствующие профили скорости звука даны на рисунках.

Универсальный метод контроля сеточных уравнений основан на использовании аппроксимирующих схем повышенной точности и применяем во всех рассмотренных нами задачах. Конечно, когда свойства среды и поля более медленно меняются вдоль оси волновода, чем в его сечении, тогда основную ошибку вносит изрезанность поля по вертикали. Эту ошибку легко оценить и проконтролировать, используя предложенный метод. В тех же случаях, когда волновод является нерегулярным, ось канала резко меняет глубину или упирается в одну из границ, волновод переходит в клин и изрезанность поля в горизонтальном направлении увеличивается, тогда метод контроля лучше применять для производных Vx, Ух поля вдоль отх.

Наконец, как мы видели раньше (см. гл. 1 и [47, 54]), используя метод выделения спектральной полосы и метод регуляризации, можно построить разностную схему, позволяющую осуществлять решение начальной задачи на сетке со сколь угодно мелкой ячейкой (/ 0,/г ->0). При этом можно добиться высокой точности, получить совпадения с соответствующей суммой распространяющихся в волноводе однородных нормальных волн, а в случае необходимости учесть и неоднородность волн.

3. МЕТОД ПОСЛЕДОВАТЕЛЬНОГО ПРОХОЖДЕНИЯ ВОЛН

В волновых задачах для гармонических волн на бесконечности должен выполняться принцип предельного поглощения. В применении к волноводам он означает, что в регулярной части волновода должны быть только уходящие на бесконечности волны. Когда мы начинаем численно решать начальную задачу для ПУГ или УГ, в решении остаются только распространяющиеся в обе стороны однородные волны. Поэтому величину обратных волн необходимо уменьшить либо при задании условий начальной задачи, либо, если приходится проходить нерегулярный участок волновода, другими алгоритмическими средствами.

Один из методов устранения обратных волн из численного решения бьш развит в [47, 54]. Это метод последовательного прохождения волн. Поясним его суть на простом примере. Рассмотрим снова одномерную задачу, когда при X < О после удовлетворяет УГ I/ (х) + U(x) = О, а при х > О и;(х) + kj и, {х) = 0. На границе л: = О имеем U{0) = Uy (0), U\0) = U\ (0). Образуем следующий итерационный процесс:

х < О X >0

/+(b+bi ...)Г (a + ai + ...)/>, (3.1)