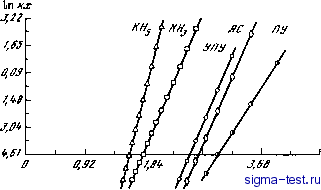-bn £

Рис. III.l. Сравнение точности схем

Используя ряд (1.33), приходим к значениям = йГо, Ъ =0,(? = 7/5!, откуда следуют оценки кНд.кь? совпадающие с (1.34). Графическое изображение этих оценок представлено на рис. III. 1.

Чтобы не усложнять изложение, мы взяли простейший случай волновода, в котором к = const. Если к -к(у)-к\ (1 + 5 р (у)) , т.е. волновод слоистый, то разность к-п надо просто заменить на Х - собственное значение соответствующей дискретной (М = 7г) задачи Штурма-Лиувилля, а е - на (Хл-о)/о.

Таким образом, если мы имеем У Г с коэффициентами к [\ + €(у)]. О < < 1, то воспользуемся разложением

Находим решение ПУ

V (X, у) = ап Фп (У) ехр [-ikx {к-КЖ к)],

где \,Фп- собственные значения и собственные функции задачи ШЛ. Ошибка Е = кх (к -Xf /(8 к)<кх к /(8k) = kx€/S. Конечно, при гипотезе о равнораспределении энергии по модам оценки сделать сложнее. Необходима асимптотика Л .

Ошибка растет вместе с ростом угла 0 =6. Нас будет интересовать случай узкого угла ±в, но не обязательно с биссектрисой вдоль оси волновода. Рассмотрим снова простейшее ПУ. Пусть нас интересуют углы вблизи (sin = По/к). В уравнении Гельмгольца Ux + уу + к U = 0 сделаем замену U = Кехр (ikox). Тогда имеем ПУГ Vxx + 2 iko Vx + Vyy + + (k-kl)V = 0. Точное решение его

F = 2 йг sin (пу) ехр (iK \/k-n-ikoK) . (1.35)

Пусть ко =у/к-По. Тогда вблизи пПо можно воспользоваться параболическим уравнением 2 iko Vx + Vyy + (к-kl) F= 0. Имеем его приближенное решение

V= 2 an sin (пу) ехр [ikoX (e-kl-n)l(2 kl)].

(1.36)

Оценим разность V-V, Полагая = о + и где 5 - малая величина, квадратом которой можно пренебречь, находим

у/к-пУ VI -2пд1(к-п1) ko(l-nobJko - nlbll2kl (1.37)

Тогда

2 sin(A2o +5 )>oSin( o +5 )exp [kx n4\l(2kl)], (1.38)

Полагая 5 =m, m = 0, ±1,... ±mo (mo < o) можно оценить ошибку в (1.38) в зависимости от величины угла 5 =то/к. Заметим, что в данном примере гипотеза о равнораспределении энергии по модам не даст значительного уменьшения ошибки, так как параметра входит в (1.38) в экспоненту всего лишь в квадрате. Однако если предположить, что -гпо <т< < то, и разложить вблизи п = По величину sin (пуо) sin (пу) = V2 [sin (у +30) -- sin (у-уо)], то мы получим в первом приближении

V-V = Аох Z т\

Ввиду нечетности целочисленной функции под знаком суммы член порядка исчезает. Поэтому V-VAixO, где в - величина узкого угла, внутри которого учтены нормальные волны, распространяющиеся вблизи угла sin 0 ~ fo/k. Были выполнены вычисления, которые полностью подтвердили полученный порядок оценки. Аналогично если вместо ПУ взять уравнение повышенной точности УПУ, то мы будем иметь ошибку либо порядка либо в.

Все эти приближения можно назвать приближениями узкого угла, биссектриса которого расположена внутри заданного широкого угла. Так как задача линейна и все поле в волноводе аддитивно складьюается из компонент пространственного углового разложения поля на источнике (или вблизи его) в интеграл или ряд Фурье, то это обстоятельство открывает возможность более точного решения задачи методом ПУ в любом широкоугольном приближении. Считая, что компоненты группируются в несколько групп нормальных волн, которые излучаются каждая внутри своего достаточно узкого угла, полагаем

где функция и по-прежнему удовлетворяет УГ, а компоненты 0, Vi ... удовлетворяют каждая соответствующему ПУ внутри достаточно узкого узла.

В связи с тем что разбиения на аддитивные компоненты по углу справедливы в любых волновых линейных задачах, такой подход справедлив в случае слоисто-неоднородных и нерегулярных по трассе волноводов. При этом надо выделить узкий угол в , величина которого входит в оценку допускаемой ошибки и другой узкий угол О, в котором задана соответствующая компонента поля - группа нормальных волн. Если волновод

является нерегулярным, то в процессе прохождения трассы эта группа волн расплывается по всему углу, определяющему величину допустимой ошибки. Понятно, что заполнение всего угла в волнами определяет тот момент вычисления поля, когда поле становится необходимо снова разложить на аддитивные компоненты внутри соответствующих углов в,

2. УНИВЕРСАЛЬНЫЙ МЕТОД КОНТРОЛЯ ОШИБКИ И УВЕЛИЧЕНИЯ ТОЧНОСТИ РАЗНОСТНЫХ СХЕМ

Контроль точности при вычислении полей самыми разнообразными методами является важнейшим условием широкого применения этих методов. Правда, иногда контроль точности представляет собой более сложную задачу, чем получение самого приближения. Найти границы применимости метода бывает гораздо сложнее, чем просто провести вычисления. Так, например, оценка применения метода ВКБ, лучевого приближения, различных асимптотических разложений практически и не делается, так как это очень сложно, требует большой гладкости границ, коэффициентов в уравнениях. Оценка применяемости МНВ, широкоугольного ПУ в неслоистых волноводах, в клине тоже не делается. Получить ошибку приближения всегда сложнее, чем обсчитать само приближение. Метод сеток, метод конечных разностей среди всех приближенных методов являются исключениями: оценить ошибку, уточнить результаты, найти границы применения сетки или схемы можно тем же самым алгоритмическим сеточным путем, которым считается поле. Можно выделить ряд отдельных этапов контроля точности и уточнения результатов.

1. Необходимо контролировать с какой точностью удовлетворяется само исходное дифференциальное уравнение - волновое, Гельмгольца, параболическое - тогда, когда функция, характеризующая поле, задана (вычислена, измерена) в дискретном семействе точек, например в узлах некоторой сетки.

2. Необходимо контролировать однонаправленность поля в регулярной части волновода, в которой поле должно состоять только из уходящих волн, если в направлении от излучателя нет нерегулярности в волноводе и на бесконечности нет источников.

3. Требуется контролировать условие на самом источнике в зависимости от того, характеризуется ли он функцией, стоящей в правой части уравнения, или функцией, заданной в качестве краевого условия.

4. В случае фильтрующих свойств волновода, особенно для достаточно протяженных трасс, когда часть волн или лучей уходит из канала, рассеивается и поглощается, их можно не учитывать при вычислении. Для приближенного устранения этих волн можно использовать направленные источники. Если же необходимо более точное описание волновода как пространственного фильтра волн, то можно вводить околоволноводное пространство. Попадающие в него волны исключаются из рассмотрения посредством ряда алгоритмических процедур.

5. Если сеточный алгоритм и разностная схема позволяют мельчить сетку, то контроль правильности вычисленного поля можно осуществлять по стабилизации вертикальных и горизонтальных разрезов поля при достаточно мелком шаге.