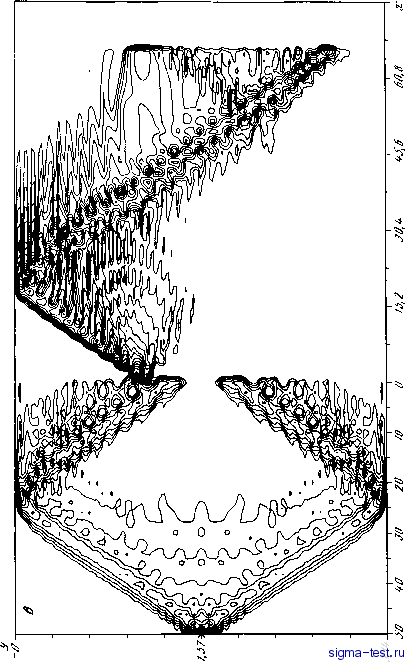Рис. I.ll. (окончание)

длина апертурного отрезка 200 м (6 узлов сетки); на рис. 1.11, в - одна частота; на рис. 1.11, г - шесть частот.

В настоящее время в практику измерения акустических полей в океане широко входят векторные приемники, т.е. приемники, измеряющие приближенно производную скалярного звукового поля в виде конечной разности на концах некоторого вектора s [58]. Векторные приемники могут быть объединены в векторную антенну, линейную или более сложную. Возникает задача, как, зная производную поля на некотором апертурном отрезке, восстановить звуковое поле в волноводе, его характерные детали, пики в окрестности источников. Выбор длины вектора и его ориентации могут быть более обстоятельно выполнен, если вместо рельефа скалярного поля, которое визуализируется в расчетах, визуализировать его соответствующую производную (конечную разность). Семейство таких векторных голограмм , зависящих от s и от самого поля, представляет большой интерес. Особенно естественно они вписываются в вычисления, выполняемые на основе трехслойных явных разностных схем, когда для нахождения поля на третьем слое необходимо знать его значения на двух слоях.

Глава II

НЕЯВНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ВОЛНОВЫХ ЗАДАЧ

Никогда не приступайте к вычислениям, пока не знаете результата.

Р. Фейман

Каждое новое изделие, процесс или услуга начинают устаревать в тот день, когда они впервые достигают самоокупаемости. Единственный путь - самому признать свое изделие устаревшим, чтобы помешать это сделать конкуренту.

1. УСТОЙЧИВОСТЬ НЕЯВНОЙ СХЕМЫ КРАНКА-НИКОЛЬСОНА

Положительные свойства явных схем для решения разностных аналогов ПУ и ПУГ несомненны. Однако ограничение на шаг / снизу при решении ПУГ заставляет рассмотреть еще один класс уже неявных схем, где это ограничение удается снять.

Для ПУ likVx уу кс - О, используя явную схему на сетке с шагами /, h получим, что шаг / может быть любым. Шаг h необходимо выбрать так, чтобы выполнялось неравенство Ikjh > max (4l~, ке). Следовательно, шаг h ограничен сверху, что не всегда удобно. Воспользуемся для решения ПУ неявной схемой Кранка-Никольсона

К(х+Л)- V(x-h) TV(x,y) = 2ik-~-- A[LlV(xh,y)

+ керсV(x + Л, V) + Ll у V{x -Ку)- кес V{x - Л, >;)] = 0.

* Десять правил, обеспечиваюпдих эффективность НИОКР БИНТИ. 1989. Т. 33. С. 41. 72