

 |
 |
|
|
Навигация
Популярное
|
Публикации «Сигма-Тест» Моделирование волновых процессов 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 [ 18 ] 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 стоящий при переменном коэффициенте в УГ, а также квадрат угла (е = = Nq) заданного пучка учтенных нормальных волн 7Vo> т.е. бугл = гидр~ = е. Известно, что требования устойчивости схемы на другой сетке Л, / для другого волнового числа к позволяют выбрать параметры h, I следующим образом: h=\lke, /=я/2/i: (10.2) Предположим, что к < к. Тогда на основании (ЮЛ) и (10.2) h > ho, / > /о. Нам известно, что разностная схема с шагом /о по оси> теряет устойчивость только при klo > 2. Поэтому, воспользовавшись выражением для /о из (10.1), находим 2 = klo = пк/2ко\/€. Получаем следующий диапазон изменения к/ко l>k/ko>W7/7i, (10.3) Для такого изменения к/ко устойчивость схемы на сетке (ho, /о) сохранится. Если же необходимо понизить частоту еще сильнее, то приходится, чтобы сохранить устойчивость, брать сетку вдвое крупнее, /о 2/о. При уменьшении частоты параметр вридр = > характеризующий неоднородность среды в УГ, остается прежним. Число же членов суммы, соответствующее учитьшаемым нормальным волнам,- приходится изменить. Необходимо суммировать только те нормальные волны, которые соответствуют лучам, лишь касающимся границ волновода - дна или поверхности. Это означает, что для фиксированной ячейки сетки, т.е. для заданного числа узлов по ширине волновода, равного 2/Vo, где No = ky/F, необходимо найти верхний предел N{k) в сумме 8i(y-yo)= i\nin{ny), (10.4) ,1=1 Раньше он был равен Ао- Теперь имеем N(k)/k = No/ко = откуда при к<ко N(k) = kNo/ko=kyj€, к<ко. (10.5) Рассмотрим диапазон устойчивости разностной схемы на фиксированной сетке при движении в сторону увеличения частоты. Для фиксированной частоты, соответствующей волновому числу ко, вместо сетки с ячейкой ho X /о возьмем сетку с более мелкой ячейкой Ло X /{>. Положим ho=a/koe. ос<1- = W/3oV >2. (10.6) Параметры а и выбираем так, чтобы устошшвость не терялась. Затем рассмотрим поле для нового волнового числа к > ко при той же самой сетке X /о. Устойчивость сохраняется при условии к<ко/а (а<1). (10.7) Число членов суммы в (10,4), равное N(k). следует заменить на величину М(к). Так как первоначальное число узлов было равно jWo, где Ло - число нормальных волн, имеем М(к)/к = No/k = лУеТ Следовательно, М(к) = ку/е, к/к о < P/2ji> 2 к> ко. Величина р была выбрана соответствующим обра- зом, когда согласно (10.6) был взят шаг меньший чем /q. Причем при 3> 2 можно положить к/ко < 1/2,к>ко. Алгоритм, использующий метод сеток для волноводных задач, оказался достаточно эффективным. Большое число задач решено и представлено на рисунках в [47, 48, 51]. Время счета Г пропорционально квадрату частоты и кубу угла учтенных нормальных волн Г=Л/t=Me/ (10.8) где А, В - некоторые коэффициенты, зависящие от быстродействия ЭВМ, шагов сетки и длины трассы. Так, например, для волновода глубиной 6 км при длине трассы 500 км, частоте 1,25 кГц И1 = 0,1 рад ЭВМ БЭСМ-6 (~ 10 операций в секунду), проходя в секунду 7-10* узлов сетки, выполняла весь расчет за 7-10 мин. Соответственно для /= 125 Гц аналогичный расчет выполнялся примерно за 10 с. Это для наиболее крупной сетки, которая обеспечивает устойчивость и дает среднюю ошибку порядка 10%. Если же точность необходимо повысить, то либо сетку приходится брать более мелкой, либо прибегать к многоточечной аппроксимации производных. При этом скорость вычисления уменьшается. Приведем некоторые примеры вьиисления полей [37, 47]. На рис. 1Лд представлено поле в канале с параболическим изменением к {к = к\{\ \-+ 6<v)) по глубине при частоте 625 Гц. На рис. 1.4, б в том же волноводе в качестве начальных значений для разностной схемы взято поле на всей глубине волновода, вьиисленное ранее. В-точке, где был локализован излучатель, поле фокусируется и дает выброс. На рис. 1.5 представлено поле направленного излучателя. При этом КО - координаты излучателя; ЯДГ, НУ - шаги по осям X и У; к - волновое число; Е = N - число шагов по ширине волновода; NK - число учтенных нормальных волн; XL - длина трассы (при ширине волновода тг); Т - время счета в минутах; F - частота. На рис. 1.6 представлено поле излучателя в волноводе с линейным профилем к; на рис. 1.7 - поле в волноводе с усеченным параболическим профилем; на рис. 1.8 - поле в волноводе с параболическим профилем и с осью канала, глубина которого меняется по синусоидальному закону <V) = { 3 - be + otM2nx/p] \/а\ Ус - а +а8ш(2ях/р) <у <Ус + аа$т(27тх/р). Поле в извивающемся волноводе представлено на рис. 1.9. Видно, как волны высвечиваются из канала в околоволноводное пространство. При вьиислении в полосе частот можно получить пространственно-частотные диаграммы звукового поля в неоднородном по трассе волноводе. Так, например, на рис. 1Л0,а приведена диаграмма к-х в волноводе с параболическим профилем при частоте 25 < / < 300 Гц. Взята часть трассы 50я < X < 150я; разрез при = я/2. На рис. 1.10,5 тот же разрез, но вводится возмущение профиля вдоль трассы по синусоидальному закону. На рис. I. 11, а-г рассмотрено поле в волноводе глубиной 3,14 км. Взято расстояние от излучателя до апертурного отрезка 50 км. Частотный диапазон 215-500 Гц. На рис. 1.11, а длина апертурного отрезка 300 м (он содержит девять узлов), движение к источнику от апертурного отрезка на одной частоте; на рис. 1.11, 5 - на восьми частотах. На рис. 1.11, в, г 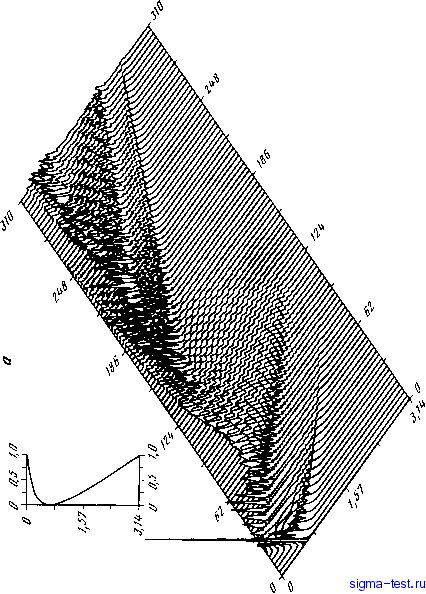
|
|
© 2010 www.sigma-test.ru Санкт-Петербург: +7 (812) 265-34-48, +7 (812) 567-94-10
Разработка и поддержка сайта: +7(495)795-01-39 после гудка 148651, sigma-test.ru(my_love_dog)r01-service.ru Копирование текстовой и графической информации разрешено при наличии ссылки. |