в качестве еще одного примера рассмотрим волновод шириной я, в котором на оси канала скорость звука минимальна, а волновое число максимально, к = к(\ + б). Введем в таком волноводе сетку, взяв на нормальном сечении число узлов N = jNq = уку/Т, i = n/N, где 7 - некоторый параметр; Nq = к\[ё - число учтенных, распространяющихся внутри угла (sini>= уб) нормальных волн в дифференциальной задаче; общее число распространяющихся нормальных волн равно к. Теперь, переходя к разностной задаче, необходимо найти угол(/?, под которым должна выходить нормальная волна некоторого номера NqNq = к), соответствующая граничному лучу, т.е. лучу, касающемуся границы волновода. Полагая в (9.3) к\ =к{\ + е), находим

2укуД -sin

Откуда

/ nki \

* (2-; Ч - ь

Сразу же видно, что если 7 < я/2, то в правой части (9.5) стоит величина больше единицы. Поэтому параметр 7 не должен быть меньше я/2. При 7 < я/2, когда

из (9.5) найти угол невозможно. Ограничение на 7 не позволяет пользоваться слишком крупной сеткой. Физически это означает, что для достаточно крупной сетки по нормальному сечению волновода конечно-разностные волны, выходя из источника, расположенного на оси канала, вообще не смогут достичь границ волновода. Волны поворачивают к оси канала гораздо раньше. Например, это происходит на том горизонтальном уровне, где к(у) = к(1 бр), бр < 6. Найдем величину ер. В соотношении (9.3) заменяем ki ткр= ks/T-ep

21- %т{кр1И%ф) .Jl? -к\ , (9.7)

2Ук . / кр-п

sm

\2y\Je

tg ]=kyfp, (9.8)

Откуда

Следовательно, при выбранном шаге / сетки, т.е. выбранном коэффициенте 7, крайние или граничные разностные волны поворачивают на том горизонте Ур сеточного волновода, на котором величина бр определяет значение :

ер = е47/я, А: =к\\ер). (9.10)

За горизонт у = Ур никакие распространяющиеся конечно-разностные волны прийти не могут. Точнее сказать, они приходят, превращаясь в неоднородные волны, но не за счет свойств среды, а за счет сетки. Это может привести к ошибкам.

Таким образом, фильтрующие свойства крупной сетки сказываются на волновом поле в сеточной среде. Никакие предположения о том, что в результате суммирования многих нормальных волн поле приобретает более гладкий характер и, следовательно, может быть аппроксимировано на более крупной сетке, не проходят.

Когда задана величина у > n/l, например y = 2,N= Iky/e , тогда находим из (9.5)

Определяем угол граничной волны:

тгу/ТТТ 4 -71: tg 0,91; tg.0,91 - .

Из этого соотношения угол <р и граничную нормальную волну Nq = к<р найти легко.

Рассмотрим преломление волн на границе сплошных и сеточных сред. В качестве одного из примеров возьмем среду, заполняющую полупространства > < 0,3; > 0. При у О среду характеризуем одним и тем же волновым числом, но в полупространствах вводим сетку с разной ячейкой.

Тогда

tg=2rirarcsin у/к - f , tgi = rcsin V - ?i (9.12)

Пусть / и /i - шаги сетки - малые величины. Воспользовавшись разложе-2

нием arcsin 2 2 + - + получаем 6

tg=y/k¥ii4k -fVm.

tgi =у/к -f/ +/5 (к-е?/т (9.13)

Сразу видно, что если li > /, то > т.е. разностный луч или, вернее, разностная волна отклоняется в сторону более крупной сетки до тех пор, пока сетка не станет такой крупной, что волна отразится назад. В другую среду пройдет только неоднородная волна.

Таким образом, было показано, что при использовании явной схемы чрезмерное мельчание сетки по нормальному сечению волновода невозможно: при kl < 2 теряется устойчивость. С другой стороны, чрезмерное укрупнение сетки тоже недопустимо: при kl > (7г/2)>/Гнормальные волны в сеточном волноводе не достигают его границ. Если же взять число узлов меньше чем число учитываемых нормальных волн, то аппроксимация поля теряет всякий смысл. Невозможно и чрезмерное увеличение шага сетки по оси волновода khe < 1. Все это позволяет вьщелить область kl, для которой выполняются как удовлетворительная аппроксимация поля, так и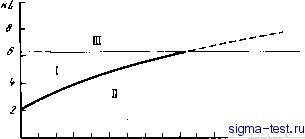

Рис. 1.3. Выбор шагов сетки h и /

I - область устойчивости ЯС при 2 < кК

ZZ 26 JOf<h

е = 0,25; II - область неустойчи-

вости ЯС и аппроксимация волн; III - схема устойчива, но поле нормальных волн не аппроксимируется

устойчивость ЯВНОЙ схемы. На рис.1.3 изображены: / - область неустойчивости явной схемы; кривая kh = f{kl) = kl\/k - Р]4 - 1 соответствует условию (1.22)

я /я я kho = -€- I- -1 =- e-*Vl-e

и - область, для которой сетка в волноводе становится настолько крупной, что волны не достигают его границ, т.е. обращаются в неоднородные волны. Небольшой островок на рисунке - это область устойчивости и удовлетворительной аппроксимации всех волн. Обычно вычисления по явной схеме проводятся в прямоугольной области D\/2e~ < kl <-у

(рисунок изображен для частного случая, когда е = 0,25). Островок D в море неустойчивости и плохой аппроксимации очень невелик. Но все же он позволяет пользоваться явной схемой, переходить для улучшения аппроксимации второй производной по > к многоточечным схемам. Эти многоточечные схемы обеспечивают в случае необходимости высокую точность, а сама сетка и ее область D обеспечивают устойчивость и препятствуют превращению однородных разностных волн в неоднородные.

10. СЕТКА В ВОЛНОВОДЕ ДЛЯ ВЫЧИСЛЕНИЯ ПОЛЕЙ В ПОЛОСЕ ЧАСТОТ. ПРИМЕРЫ ВЫЧИСЛЕНИЯ ПОЛЕЙ

Рассмотрим диапазон усттойчивости разностной схемы на фиксированной сетке при движении в сторону уменьшения частоты. Возьмем некоторую фиксированную частоту cjq, соответствующую волновому числу ко. Для разностного аналога ПУГ AF + kleV + 2ikoVx = О выберем сетку в волноводе с ячейкой /о X ho. Шаги /о, ho определим согласно соотношениям

ho = 1/(ко€), /о = n/lkoy/iy (10.1)

при которых разностная схема устойчива. В (10.1) е - малый параметр.