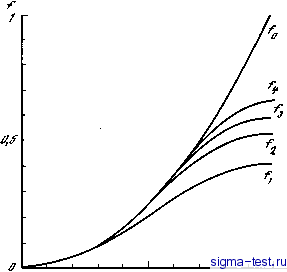Рис. I.l. Графики функций/q

Д - точное решение; /j -Д - решение на трех-, пяти-, семи- и девятиточечном шаблоне

Тогда решение УГ (3.10) имеет вид

йХуу) = \ sin(A2>)exp[bcV -(4 2)sin(A2 2)]. =i

(3.12)

Оно отличается от (3.2) очень существенно. Во-первых, тем, что под корнем вместо гР стоит величина 4/ sin 2, а во-вторых, тем, что сумма стала конечной. Поэтому, ограничивая шаг / снизу неравенством

Ы > 2, (3.13)

можно исключить из рассмотрения неоднородные затухающие и нарастающие волны. Это сделает начальную задачу для (3.10) устойчивой, а число узлов TVna интервале будет ограничено сверху к/М>2/7Г,

Что касается аппроксимации целых величин п (п = 1,2,...) функциями 4/ sm(nl/2), то такая аппроксимация лучше всего выполняется на интервале п < к, т.е. когда n/N = д <1 (см. рис. 1.1). Так как nfk = sint , где t - угол скольжения нормальной волны а2-го номера вдоль границ волновода. Поэтому тогда, когда углы скольжения всех предствляющих интерес нормальных волн невелики, замена величиной 4/ sin(A2 2) вполне оправданна. Например, если <\/Т[е<1), то полагаем для числа узлов

N = 2ку/Г. (3.14)

Имеем kl = 7г/(2\/ > 2 при б < 7Г16.

Вводя сетку с шагом h вдоль оси jc и с шагом / вдоль оси у можно рассмотреть разностное УГ

(Ll + + к)и = 0. (3.15)

Его решение предствим в виде конечного ряда

и(х,у) = S /3 sin(A2>)exp(/K/,jc). (3.16)

Подставляя (3.16) в (3.15), находим характеристическое уравнение

(-4 z)sin(/c /2)-(4 )sin(A2 2) + A: = О а2=1,..., N-1, (3.17)

Все величины Кх ... Kjii - корни уравнения (3.17) - будут вещественными, если kl > 2,kh < 2, т.е. выполняются неравенства (1.5) и (3.13). При этих условиях неоднородных волн в сеточном волноводе не возникает. Схему (3.15) можно записать в виде

[uix+Ky)-\-u(x-h,y)]lh + [w(x,7 + /) + w(x,.v-/)] + + (k-2/h -2lf)u{x.y) = О (3jg)

или в виде

uix-Ky) = aw(jc,>0 + /3[w(x,V+/)+w(x V-/)] -u(x-h,y), (3.19)

где коэффициенты а, /3 легко найти из (3.18). Сразу видно, что эта схема пятиточечная. Она связывает и(х, у) в пяти соседних узлах сетки, расположенных крестом (схема крест ) : х, у; х±К у; у ± /. Схема (3.18) трехслойная, так как связывает и{х, у) на трех слоях - трех нормальных сечениях волновода х - h, х, х h. Схема явная, так как новое значение и{х + /г, у) в узле на третьем слое находится в явном виде по формуле (3.19) через значение и{х, у) в четырех узлах на двух предыдущих узлах. При этом согласно (3.19) необходимо выполнить два умножения и три сложения, вообще говоря, над комплексными величинами, характеризующими поле.

4. ТРЕХМЕРНЫЙ СЛОИСТО-НЕОДНОРОДНЫЙ ВОЛНОВОД

Уравнение гармонических колебаний для звукового давления Р в трехмерной неоднородной среде с переменной скоростью с{х, у, z) звука и плотностью р(х, у у z) имеет вид

pV(p VP) + kP = F(x,.v,z), (4.1)

где V = i - + j - + к - ; = со/с(х,у, z) \ F - функция, характе-

Ъх Ъу bz ризующая источники. Путем замены =iV7 (4.1) приводится к УГ (Д =V )

Aq + [к +\/pV(p Vp)] = Fp\ (4.2)

Поскольку Vp \7(р 2 Vp) = Ар - %)p~(Vp), то член {Vp/pf имеет один и тот же знак при флуктуации плотности вблизи среднего значения. Из (4.2) видно, что изменение плотности приводит к изменению коэффициента К1ф в УГ Д + эФ~ касается источника, то он в ряде задач бывает точечным ненаправленным F = 8(х - Хо)д(у - Уо)8{г - Zo), где 5 - функция Дирака.

Трехмерные волноводы могут быть цилиндрическими, т.е. с нормаль-

ным сечением в виде односвязной или более сложной плоской фигуры (например, ВОЛС). Они могут быть и в виде слоев, как, например, в сей-смике. Однако наиболее интересным случаем трехмерного слоистого волновода является подводный звуковой канал - ПЗК.

В трехмерном слоистом звуковом волноводе в океане интерес представляет наиболее хорошо изученный и чаще всего встречающийся случай, когда рис зависят только от глубины z, а излучатель, характеристика направленности которого изменяется только в вертикальной плоскости, расположен в точке х = у = О, z = Zq, Этот случай подробно исследован в [20, 22]. Вводя цилиндрическую систему координат г, t, z (r = х +.v) и предполагая, что поле не зависит от угла t, имеем двумерное У Г на плоскости г, Z

Ргг + (imPzz k\z)P = 0. (4.3)

В правой части (4.3) стоит нуль, так как при численных решениях (4.3) 5-образный источник можно учесть в виде начального условия при г =0. Полагая в (4.3) P-r~u{r,z) имеем

Член 1/(4/*) не дает вклада в поле на расстояниях, превышающих несколько длин волн. Пренебрегая им, находим окончательно

Ъи/Ъг = -(к + aVaz)w. (4.5)

Двумерное УГ (4.5) с переменным коэффициентом к (z), а в более общем случае для волноводов, переменных по трассе - к (г, z), является основным уравнением, для которого рассматривалось конечно-разностное приближение. Для решения его используются параболическое приближение, разные другие пути аппроксимации оператора в правой части (4.5), о которых было подробно рассказано выше (см. введение, разд. 5).

5. ЯВНАЯ СХЕМА ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА В СЛОИСТО-НЕОДНОРОДНОМ ВОЛНОВОДЕ

Приведенные выше простые примеры и оценки можно использовать и в конкретных, более сложных случаях. Рассмотрим в полуполосе х > О, О < V < я задачу для У Г с переменным коэффициентом

txx + tyy + [1 + Ф)] W = О, W 1 = f(y), и I = О,

где к, € - вещественные положительные величины; ip(y) - вещественная функция, принимающая значения от О до 1: О < < 1. Пусть /(у) = ~ 5(у - уо). Это означает, что в точке у = уо на границе х = О находится источник звука. Будем считать, что слоистая среда, заполняющая волновод, имеет минимальное значение скорости звука на оси канала тоже при У Уо- {Уо ) = 1. На границах волновода скорость максимальна, а к минимально: iflo) = (/?(я) = 0. То, что источник находится на оси канала, не является существенным, но упрощает вид геометрической картины лучей, выходящих из точки у = Уо- При этом по закону Снеллиуса Р (1 + e)cos = , где ± 10 - углы выхода двух лучей из точки у =Уо,