бимолекулярными. Функция Ф одновременно отражает зависимость плотности от Т. Разделим обе части уравнения (5-10) иа величину Cf = cpjkT, где -газовая постоянная. Тогда второй член, соответствующий теплу, выделяющемуся при реакции, оказывается пропорциональным р ~ и Ф{Т)-Т. Получающееся таким образом выра-нгение можно записать в виде Zp~f(T).

Характер протекания функции f(T) имеет большое значеине. Некоторые свойства этой функции могут быть найдены из самых общих сообрая:ений. Напри.мер, известно, что при очень низких температурах реакция но существу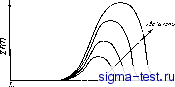

ТвмпЕратура, С

Рнс. 5-,1 Обтай фор.ча крнаых выдс,:сннн прн роакцнах.

не идет, т. е. если Т мало, /(Г) = 0, Если Т приближается к - температуре продуктов сгорания, то скорость реакции опять уменьшается в связи с уменьшением концентрации реагентов, поэтому /(?(,) = О, Таким образом, качественно протекание функции Л/(Г) должно быть таким, как это изображено на рис. ,5-3. Скорость реакции растет с гемггерагуроя, поэтому по мере повышения уведичн-вается также максимальное значение функции. В случае при-Меиимости уравнения (5-9) кривые графика могут быть получены расчетом. Общий анализ формы этих кривых показывает, что величину Z можно рассматривать как меру максимальной скорости выдсаения тепла, т. е. высоты подъема кривых, а функция /(Г) определяет наклон кривых.

Графический метод решения. Если реакция вообще не протекает, то уравнение (5-11) переходит в

(5-12)

Это уравнение одномерного пестацноиарного pacnpoeiранения тепла при иоетоянно1 тен.топроводности и отсутствии источников и стоков. Для решения утого уравнения можно использовать аналитические, численные и !рафнче-скне методы. Однако при наличии реакции имеются источники тепла. В этом случае аналитические решения обьтно невозможны и приходится использовать числеииые и гра-)ические методы iSpalding, 1953, Ь). Эти методы для случая одномерного распространения тен.ла весьма подробно рассмотрены Дюсинберре (Diisinberre, 1949). При таких расчетах среда предпо.тагается состоящей из ячеек конечного размера, в которых непрерывное изменегше температуры вследствиетеилоироводиости заменяется скачкообразным изменением по интервалам времени. Подобный метод расчета, пригодный также для случая изменения температуры в результате реакции, изложен ниже.

Заменяя дифференциальное уравнение (5-11) уравнением в конечных разностях, которое дает связь между значениями температуры в точке m в моменты времени п и /Н-1 с значениями температуры в соседних точках тл-\ и т-1, по,лучим:

+ Zp -4iT ,)M. (5-13)

где подстрочные индексы п и т. д. относя геи CJOTBer-сгвеннпо к точке и моменту времени;

Дх -ширина ячеек, на которые разбивается среда;

Д?-конечный интервал времени.

Величины и Д; .могут быть выбраны про 13вольио, однако их удобно выбрать так, чтобы (аД/)/(Д) -Y- как в этом случае уравнение (5-13) переходит в

Г = 1?±М± (5-U)

Отсюда с. 1едуе1. что температура в слое т в момент времени +1 равна средней арифметической температур в соседних слоях пг-1 и /7/-ь1 в предыдущий момент времени плюс некоторое повышение в результате протекания )еакцин, зависящее от температуры в соответствпи с принятым законом скорости реакции.

Выражение (5-14) дает возмож110С1ь разработать простой численный метод расчета пространсгвенного распре-2Щ

к-.-кчтя -гомпоратуры, получающегося нз нс\оди(И () состоя-1ия после неокатьких последовательных интервалов времени. Л1ь будем пользоваться графическим методом, подобным методу, который для одномерного случая задачи о распространении тепла известен как метод Ш.мидта (Schmidt, 1924). Однако в предлагаемом методе учйты-сасКя не только передача тепла теплопроводностью, но и выделение тепла в результате химических реакций. Несмотря на нриближен}1ость метода, его точность в даиггам случае достаточна.

Р й 3 в И т п е стационарного п .1 а м е п и. Применим изложен!1ЫЙ метод для изл!ения развития стационарно распространяющегося пламени от некоторого начального состояния, при котором больпюй объем продуктов сгораиия соприкасается плоской поверхностью с большим объемом горючей смеси. Под большим объемом подразумевается обт>ем, размеры которого значительно больше, чем шири1!а фронта илам-ни. В начальный момент времени профиль температуры в плоскости, перпендикулярной поверхности соприкосновеш1я объемов, имеет прямоугольную (юрму и на рис. 5-4,а обозначен цифрой 0. Последующие профили температур, найденные графнчески.м методом, представлены ломаными линиями с I но 10. которые приближенно соответствуют в действительности плавным кривым распределения температуры.

Заданный злкон скорости реакции, т. е. изменение Zp ~l\T)\i по Т, представлен иа рис. 5-1,/?; масштабы (го осям абсцисс и ординат одинаковы.

Кривые /-4 показывают, что около исходной граничной плоскости температура продуктов сгорания падает, по после момента времени 4 она снова начинает возрастать; кривые, соответствующие последующим моментам Бремени, во избежание затемнения чертежа показаны на рис. 5-4,6. Окончательный профиль температуры сохраняет приблизите, тьно постоянную форму и перемещается вправо с постоянной скоростью, Это состояние соответствует стационар-пому распрострапеинга полностью развившегося нламени.

Хотя закон скорости реакции был задан произвольно, ли1жп0 тем не менее сделать определенные выводы о зависимости скорости распростра1!е1П-1я 5 от некоторых факторов. Заданной кривой, нзобрал<енной па рис. 5-4,5, соответствуют единственное реп1сиие и соответственно онреде-.тенная скорость распространения пламени. Таким образом, для того чтобы стационарно распространяющееся пламя