должна быть перемешана с единицей массы текущей жидко-егн, для того чтобы получить смесь, обладающую теми же специфическими свойстБами, что и свойства жидкости в не-1Н1средственнон близости к поверхности.

Эта теорема, следствия которой будут рассмотрены ниже, имеет особое значение для расчета движущей силы при наличии химических реакций. Разъясним теперь указание на снсцнфнческие свойства на примере анализа ироцес-еов одновременного протекания тепло- и массообмена.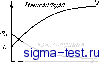

Одновременное протекание тепло- и массообмена

Массообмеи лишь в редких случаях не сонровождается ичпообменом. При испарении жидкости в потоке газа она обычно имеет более низкую температуру, чем газ; следовательно, тепло передается от газа к жидкости. Если один пз компонентов газовой смеси поглощается жидкой поверхностью, 10 выделяющееся в процессе рас-1-иорения тепло вызывает некоторое повышение температуры жидкости (по сравнеи1Н0 с температурой газа). При горении жидких и твердых топлив тенло-обмеи играет, по крайней мере, такую же роль, что и массообмеи.

Испарение. До сих Нор при изучении массообмена наше внн-Ман]1е было сосредоточено иа из-ме[еиин концентрации переносимого вещества. Рассмотрим теперь дополнительно изменение энтальпии. На рис. 3-10 скематически показаны профили концентрации и температуры у поверхности испаряющейся жидкости.

Конвективный театообмен в установтгвшемся ламинарном потоке подчиняется уравнению (3-4). Преобразуем это уравнение аналогично тому, как это сделано иа стр. 79 при рассмотрении граничных условий. Величину нормальной составляющей скорости у поверхности найдем из теплового баланса;

Расстоянир noefiprMacmu

Рис. 3-10. Распределение температуры и концентра-оверхностн испаре-нпя.

Ц(И1

А гат \

(3-67)

где Q - количество тепла, отведенного от газа, па едн-Нщу массы испарившейся жидкости;

(Jfy -градиент гetпepaтypьl на новерхностн (по пормал к ней);

X - коэффициент теплопроводности газа,

Если произвести подстановку Ь--, где с - удельная

теплоемкость газа прн постоянном давлении (принята*, неизменной), то легко показать, что уравнен[1я (3-4) if (3-67) преобразуются соответственно в основные дифферен циальные уравнения и граничные условия, приведенные на стр. 79, с той только разницей, что D надо заменнтк

коэффипиентом температуропроводности a(=-~j. Oj

сюда следует, что, как и раньше, движущая сила массообмена дается выражением

где индекс Н у велич1шы В указывает, что последня; получена из баланса тепла; и - соответственно теш перагура в т[Отоке жидкости и на поверхности. В отличСи! от Bf обозначим через парал1егр переноса, полученнЦ из рассмотрения баланса массы: В~(т - mjjim - 1 (см. стр. 81), где т обозначает концентрацию .тнффун рующего вещества.

Оба выражения для В применимы одновременно. На дем связь между шши из условия, что перенос .MacCi может осуществляться в любой момент времени тольк с одной единственной скоростью. Как известно, эта ск рость пропорциональна как Ф (В Sc), так и Ф (В , Pi (критерий Прандтля заменяет критерий Шмидта, если заменяет D). Следовательно, обе функции должны бы% равны между собой. Используя приближенное логарифми ческое выражение для функции Ф, найдем:

Dln (1 + В ) = а- In (1 + В ), (3-69

Из уравнения (3-69) mohvHO сделать следующий ввжнЩ вывод: если коэффициенты переноса тепла и веществ одинаковы (это условие приближенно выполняется дл обычных газов), то В = В. Физически это означает, чТ состав газа и температура у поверхности имеют таки значения, какие могут быть получены путем смешенк 96

1;.(1)встсгвую[ЦСй массы персноспмиги вещества с единицей массы исходной жидкости. Возвращаясь к теореме предыдущего раздела, можно теперь утверждать, что па-р;1я1етры переноса, оигосящиеся к различным свойствам )КИДКОСти, од[1наковы, если рав!1Ы коэффициенты переноса

д,;1Я этих свойств.

Можно показать конгруснгность уравнения (3-68) и рассмотренной выше теоремы, если учесть, что при изменс-йни температуры единицы массы от до она теряет количество тепла, равное с{Т - TJ. Так как для испарения единицы массы переносимого вещества требуется Q ед11ниц тепла, то количество испаренного вещества будет равно c(TTJIQ.

Психрометр с влажным и сухим термометра si и. Уравнение (3-69) даег связь между температурой И \онцентрацпей переносн.чого вещества на поверхности. В качестве примера, иллюстрирующего применение этого ур;1внения, рассмотрим психрометр с влажным и сухим термометрами, позволяющий определить влажность воздуха но разности между температурой воздуха и температурой поверхности воды, испаряющейся адиабатически в воздух. Под адиабатическим испарением подразуме-iraeicH испарение при наличии теплообмена только между водой и газом.

Для простоты примем, что для смеси водяного пара с воздухом 0 = аточнее, ~ = 0,87J. Тогда из уравнения (3-68) нолучи.м:

-- (3-70)

Где т - масса водяного пара в единице массы паровоздушной смесн; L - скрытая теплота испарения воды, заменяющая всчичину Q (она равна количеству тепла, подведенного от газа к жидкости при адиабатическом испаре[Н!И). В этом уравпенпи Т н - температуры, измеряемые

посредственно термометрами, а L п с (средняя удельная

плпемкость воздуха при постоянном давлении) - изве-

стньк- величины.

Далее можно принять, что воздух вб,чизн жидкой по-РХ[Ости насыщен водяньпл! пара.ми и, следовательно,

в. Спо,Дянг У7