Затем из нижнего положения крыло под действием упругих сил начнет двигаться вверх с ускорением. Возникшие при этом инерционные силы приведут к закручиванию крьша на положительньш угол Дар и к появлению, следовательно, возбуждающей силы АУ, направленной в этом случае вверх. Вследствие вертикальной- скорости произойдет изменение шправления результирующей скорости набегающего потока на величину отрицательного угла атаки Дйиз, что вызовет появление дополнительной, направленной вниз, демпфирующей силы ДУд. Пройдя.через нейтральное положение, крьшо начнет раскручиваться в обратную сторону. Затем опять из верхнего, положения крьшо под действием упругих сил начнет двигаться вниз, и рас- смотренная картина повторится. ,

Точно такая же картина будет, если первоначальным импульсом будет не импульс изгиба, а импульс кручения. Здесь при закручивании крьша пбявится возбуждающая аэродинамическая сила, которая вызовет колебания крьша.

Если возбуждающие силы будут больше демпфирующих, то крыло за счет силы, представляющей их разность, получит дополнительный импульс, привЬдящий к увеашчению амплитуды изгиба и кручения. При этом чем больше расстояние между фокусом и центром масс, тем больше при прочих .равных условиях будут амплитудь! кручения и больше будет величина возбуждающих сил. Если же демпфирующие силы будут больше возбуждающих, колебания будут затухать.

При рассмотрении физической картины флаттера бьшо сделано допущение, что. частоты изгибных и крутильных колебаний совпадают, а максимумы их амплитуд сдвинуты относительно друг друга на четверть периода. В реальных условиях и частоты будут различными и сдвиг будет иньгм, но картина флаттера будет мало отличаться от рассмотренной.

На рис., 32 приведены графшси работ возбуждающих и демпфир>я)щих сил за один период колебаний в зависимости от скорости полета V. Участрк Оа на графике представляет работу сил внутреннего трения в эле?те1ггах конструкции, не зависящую от скорости полета. Так как возбуждающие силы пропорциональны квадрату скорости, а демпфирующие - скорости в первой степени, то графики их работ при каком-то значении скорости пересекутся. Скорость, при которой работы возбуждающих и демпфирующих сил становятся равными, называется критической скоростью флаттера - Уфд. При скоростях полета, меньших Уфд, работа демпфирующих сил больше работы возбуждающих сил и поэтому колебания будут затухать.

Линия ippKycoB

Осьжесткости

Работа дозбуждаю-щил сил

Работа демп-. /рирующих сил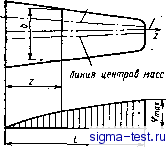

Рис. 3.2. Зависимость работы возбуждающих и демпфирующих сил от скорости полета

Рис. 3.3. Расчетная схема крыла для определения критической скорости изгибно-крутильногр флаттера

При скорости полета, равной критической скорости флаТтера, колебания происходят с постоянной амплитудой. При скоростях полета, больших Уфд работа возбуждающих сил больше работы демпфирующих сил, что приводит даже при самом малом импульсе к усилению колебаний. Быстрое возрастание в этом случае амплитуды колебаний влечёт за собой разрушение крьша. Поэтому необходимо, чтобы критическая скорость флаттера была больше максимально .возможной скорости полета самолета.

Рассмотрим влияние отдельных параметров на критическую скорость изгибно-крутильного флаттера.

Для этого оценим прнолиженнр ее величину на примере крыла, показанного на рис. 3.3. Так как при изгибно-крутильном флаттере преобладающей формой колебаний является крутильная, будем считать, что прогибы ртсутствуют. Это станет возможным тогда, когда возбужающие силы ДУ будут равны силам инерции рин- От сил ДУв и рин= Дв крыло будет закручиваться моментом

Мкр = /ДУвГ(12,

или после подстановки значения ДУв

мкр - с

р- 1,у/AuKpbrdz.

Пусть угол закручивания по размаху крьша меняется по закону Дкр = atjmax ,

где imax - максимальный угол закручивания на конце крыла; А - какая-то функция, зависящая от z. ,

Из строительной механики тонкостенных конструкций известно, что угол упругого закручивания

. = /dz, .

о GJ кр

где GJ кр - жесткость кручения,

Максимального значения этот угол достигнет на конце крыла

= } Мкр

Подставив значение М,<р с учетом принятого закона изменения, угла -закручивания в выражение для imax. найдем критическую скорость флаттера

фл = \[.

J кЬхйг

Анализ этой формулылозволяет сделать следующие вьшоды. 1. Повышение жесткости крьша на кручение GJ кр увеличивает критическую скорость. Повышение GJ р происходит при уменьшении удлинения

рис. 3.4. определение угла атаки поточного сечения стреловидного крыйа при его деформации

Ось жесткости

Пания прогъбов оса жесткости

крьша и увеличении относительной толщины и сужения. Кроме того, с увеличением сужения уменьшаются размеры концевых хорд, а следовательно, уменьшаются величины аэродинамических и инерционных сил на наименее жестких концевых участках крьша, оказывающих наибольшее влияние на флахгер.

2. Изменение изгибной жесткости крыла маловлияет на величину Уфд.

3. Уменьшение расстояния между фокусом и центром масс г увеличивает критическую скорость. Основным конструктивным мероприятием, предотвращающим возникновение изгибно-крутильного флаттера, является создание конструкции с возможно более передним положением центра масс. В случае необходимости смещение-вперед центра масс достигается дведением дополнительных балансировочных грузов, располагаемых в носке крыла. Наиболее эффективной является постановка таких грузов в носке концевой тасти крыла, где ускорения наибольшие и требуемый результат поэтому достигается при меньшей массе груза.

4. Перемещение центра жесткости пракпгчески не сказывается на величине критической скорости. Смещзкие оси жесткости вперед ведет к увеличению момента инерционных сил и уменьшешио момента возбуждаюищх аэродинамических сил, и, наоборот,-смещение оси назад увеличивает момент возбуждающих аэродинамических сил и уменьшает момент инерционных сил, оставляя практачески без изменения суммарный крутящий момент.

5. С ростом угла стреловидности увеличивается критическая скорость. На стреловидном крыле углы атаки сечений, параллельных потоку, изменяются не только из-за деформации кручения, как в прямом крыле, но и из-за деформации изгиба.

Рассмотрим парал-лельное потоку сечение 1-2 (рис.3.4. При изгибе крьша вверх это сечение повернется и займет поло5кение l~2 . Угол атаки его при этом уменьиштся. Обратная картина будет при изгибе крьша вниз. Обозначим вектором изменение угла атаки сечения 3~4 при кручении крьша относительно оси жесткоста, и вектором df/dz - наклон этого сечения при изгибе й£И жесткости. Спроектировав эти векторы на ось, перпен-, дикулярную плоскости сечения 1-2, найдем изменение угла атаки этого сечения при деформации крьша:

Да = ip, COSX

Следовательно, изгиб стреловидного крьша приводит к благоприятному с точки зрения флаттера изменению углов атаки сечений, при- этом чем больше будет угол стреловидности, тем больше будет и критичес-. кая скорость.

6. Увеличение высоты полета ведет к росту Уфд.

7. Сжимаемость воздуха влияет на величину Уфд через параметры с, и г . На сверхзвуковом режиме с ростом числа М уменьшается с и вследствие смещения назад фокуса - г , что приводит к увеличению Уфд.

8. При больших сверхзвуковых скоростях полета вследствие кине*и-ческого нагрева происходит-уменьшение модулей G и Е,а следовательно, снижается и жесткость крыла на кручение и изгиб, что приводит к уменьшению критической скорости флаттера.

ИЗГИБНОЗЛЕЮННЫЙ ФЛАТТЕР

При рассмотрении физической картины изгибно-злеронного флаггера предположим для упрощения, что крыло является абсолютно жестким на кручение и упругим на изгиб что элерон не имеет весовой балансировки, и следовательно, его центр масс расположен позади оси вращения.

Пусть крыло, как и в предыдущем случае, под воздействием какого-то возмущающего импульса прогнулось вверх (рис. 3.5). Затем под действием возникшей упругой силы Рупр крыло с ускорением начнет возвращаться к своему нейтральному положению. Появившаяся при этом инерционная сила элерона Рин.эл, приложенная в его центре масс и направленная в сторону, обратную ускорению, т.е. вверх, создаст относительно оси вращения шарнирный момент

~ Рин.эл а,

где а - расстояние от центра масс элерона до его оси вращения.

Под .действием этого момента, из-за упругости проводки управления или наличия люфтов в ней либо При свободной ручке элерон отклонится вверх. Отклонение элерона эквивалентно изменению угла атаки на какой-то отрицательный угол Даэкв- В результате возникнет дополнительная аэродинамическая сила, направленная вниз в сторону движения.

Величина этой возбуждающей силы на единицу длины крьша будет

Вследствие вертикальной скорости движения крыла u=df/dt, как и в предыдущем случае, появится дополнительная аэродинамическая демп-фирующа сИла, величина которой на единицу длины крьша будет равна

Имея запас кинетической энергии, крыло пройдет нейтральное положение и из-за сопротивления, оказьшаемого упругими силами, начнет двигаться с замедлением. Под действием возникших при этом инерционных сил элерон начнет возвращаться к своему нейтральному положению. Затем из нижнего положения, под действием упругих сил, крьшо начнет двигаться с ускорением вверх, а элерон под действием инерционных сил отклонится вниз. Такое отклонение элерона вызовет опять появление дополнительной аэродинамической силы, совпадающей с направлением движения, т.е. возбуждающей силы. Одновременно вследствие вертикальной скорости возникнет и демпфирующая сила. ,

При некоторой скорости, полета, называемой критической скоростью изгибно-элеронного флаттера Уфд, работы возбуждающих й демпфирующих сил станут одинаковыми (см. рис. 3.2). При скорости, превышающей

цм элерона \ ось вращения - окус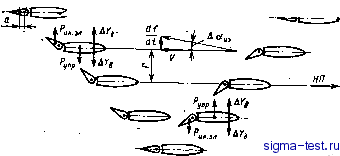

рис. 3.5. схема возникновения изгибно-элеронного флаттера крыла

рис. 3.6. формы изгибно-элеронного флаттера

уфл, работа возбуждающих сил будет больше работу демфирующих сил, изгибные колебания начнут происходить со все возрастающей амплитудой, что повлечет за собой разрушение крьша.

Различают две форми изгйбно-элеронноо флаттера:

1) симметричная, когда оба элерона отклоняются в одну и ту же сторону вследствие упругости проводки управления,или наличия в ней люфтов (рис. 3.6,а);

2> антисимметричная, когда элероны отклоняютсяв разные стороны,что может произойти при свободной ручке (штурвале), а также вследствие упругости в проводке управления или наличия в ней люфтов (рис. 3.6, б). Каждой из этих форм соответствует своя критическая скорость.

Основной причиной возникновения злеронных видов флаттера является несбалансированность элеронов. Поэтому основным конструктивным мероприятием, увеличивающим критическую скорость флаттера, является весовая балансировка элеронов.

Увеличение жёсткости крьша на изгиб и кручение, устранение люфтов в проводке управления и повышение ее жесткости также ведет к росту критической скорости.

§ 2. ДИВЕРГЕНЦИЯ

Аэродинамические силы, действующие на находящееся в потоке воздуха крьшо, вызывают его изгиб и закручивание. ДефОрмащся крьша приводит к изменению угла атаки. Изменение угла атаки, в свою очередь, приводит к изменению аэродинамических сил. Этот процесс будет продолжаться до тех пор, пока не наступит равновесие. При какой-то скорости полета такое

равновесие становится невозможным, деформация (главным образом,деформация кручения) растет, и крьшо разрушается.

Явление перекручивания крьша, при котором аэродинамические моменты относительно его оси жесткости растут быстрее восстанавливающих упругих моментов, что приводит к разрушению конструкции, назьшается дивергенцией. Скорость полета, начиная с которой статическая устойчивость конструкции оказьшается невозможной,называется критической скоростью дивергенции. На примере изображенного на рис. 3.7 крыла рассмотрим условия, при которых возможна дивергенция

В поточном направлении 7-2 выделим участок длиной dz вдоль оси жесткости. На этот участок действует подъемная сила dvg и сила лобового сопротивления dxa , приложенные в фокусе, и момент относительно фокуса dMj q. Спроектировав cHnbi dya ndXg на хорду 41 на нормали к ней, получим силы dN и dT. Тогда момент сил, действующих на рассматриваемый участок, относительно оси zi, перпендикулярной поточному сечению и проходящей через центр жесткости, при пренебрежении моментом от силы dT пишется в виде

dM(z,) =dNr +dm30,

где г - расстояние от фокуса до центра жесткости в поточном сечении.

Полет на максимальной скорости осуществляется намапых углах атаки, при которых dN dya . -

Подставив значения

dya = Су (а + cosx - -inx)-bdz cosx

dmao = obdzcosx

a 2

получим ДЛЯ dM(2 следующее выражение;

*(2i) = [Суа (a+cosx-smx)r+ СпудОbjbdzcosx

Зная dM

жесткости в.любом сечении:

можно определить крутящий момент отнрсительно оси

мкр = / dmkp,rfledmkp= dm(j) cosx. подставив значение dm , получим

мкр =

cosx/[cy (а+ сох- sinx) г + с ob]bdz.

из стюительной механики тонкостенных конструкций известно, что угол упругого закручивания . .

= / .ХР

-dz.

о кр Где gj кр жесткость кручения.