подобных диаграмм приходится проводить гиперболу через данную точку.

При заданной точке М построение сводится к следующему. Через точку М проводят вертикальную прямую ML и горизонтальную АВ. На прямой ML выбирают произвольные точки, например 7, 2, 3, 4, 5 и т. д., через которые проводят горизонтальные прямые. Из начала координат О через те же точки проводят ряд лучей. Из точек пересечения лучей с прямой АВ (I, II, III, IV и пр.) опускают перпендикуляры на горизонтальные прямые соответствующих номеров. Точки пересечения этих перпендикуляров с горизонтальными прямыми и будут принадлежать гиперболе.

Построение политропы (рис. Ш.47,в). Политропой называется кривая, выражаемая уравнением jx = с, где с - постоянная величина. Эта кривая применяется при построении индикаторных диаграмм тепловых двигателей, причем показатель п заключается в пределах 1,1 - 1,4. При п=1 кривая превращается в равнобочную гиперболу. При п = 1,4 кривая называется адиабатой. Для построения политропы, проходящей через заданную точку М и имеющей показатель п (рис. 111.47,б), проводят прямую О А под произвольным углом а к оси ОХ и прямую ОВ под углом р к оси О У. Угол р определяют из уравнения tgp = (1-Ь tga) -1. Далее через точку М проводят горизонтальную прямую до пересечения с осью ОУ в точке а и вертикальную линию до пересечения с прямой О А в точке Ъ. Из точек а и b проводят под углом 45° к осям прямые, пересекающие линии ОВ и ОХ в точках end. Перпендикуляры к осям, проведенные через эти точки, дают на пересечении точку 1, принадлежащую политропе. Так же находят и следующие точки (2, 3, 4 и пр.).

Построение синусоиды (рис. III.48). Для построения синусоиды делят данную окружность на произвольное число равных частей; на такое же число равных частей делят отрезок прямой АВ, равный длине данной окружности (2nR). Проведя через точки деления горизонтальные и вертикальные прямые, на пересечении их находят точки синусоиды.

Кривые, изображающие гармонические колебательные процессы, тоже имеют вид синусоид и строятся подобным образом. Однако в этом случае период полного колебания АВ может быть не равен 2nR.

Построение цилиндрической винтовой линии (рис. III.49).

Фронтальная проекция строится так же, как синусоида. Окружность, являющуюся горизонтальной проекцией цилиндра, делят на равные части; на столько же частей делят заданный шаг (?) винтовой линии. На пересечении одноименных фронтальных и горизонтальных линий получаются точки

винтовой линии. На рис. П1.49 показана левая винтовая линия; если видимая часть винтовой линии поднимается в направлении слева направо, то ее называют правой.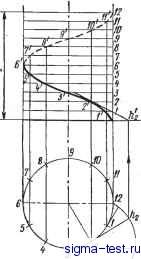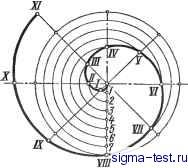

Рис. III.49. Построение цилиндрической винтовой линии

Рис. III.50. Построение спирали Архимеда

Длина одного витка винтовой линии

/= 1/?Т(2,

т. е. она равна гипотенузе прямоугольного треугольника, катетами которого являются шаг t и длина окружности основания цилиндра 2nR. Горизонтальные следы касательных к винтовой линии располагаются по эвольвенте. Для построения касательной в точке 2, например, надо провести горизонтальную проекцию 2~h2 касательной и затем найти вертикальную проекцию точки 2, т. е. /г, и соединить точки 2 и /г.

Построение спирали Архимеда. Спираль Архимеда - траектория точки, движущейся с постоянной скоростью от центра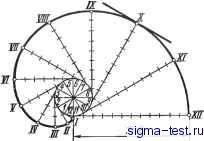

Рис. III.51. Построение эвольвенты окружности

окружности по радиусу, вращающемуся также с постоянной угловой скоростью (рис. III. 50). Для построения ее радиус окружности и окружность делят на одинаковое число равных частей; лучи проводят из центра через точки деления окружг ности. Откладывая на первом луче одно деление радиуса, на втором - два и т. д., получают ряд точек спирали, которые затем соединяют по лекалу.

Построение эвольвенты (развертки) окружности. Для построения развертки (рис. III.51) окружность предварительно делят на произвольное число равных частей. В точках деления проводят касательные к окружности, направленные в одну сторону. На касательной, проведенной через последнюю точку деления, откла-дьшают отрезок, равный длине окружности Q,nR), и делят его на то же число равных частей. Откладывая на первой касательной одно деление окружности, на второй - два, на третьей - три и т. д., получают ряд точек /, II, III, IV и т. д., которые соединяют по лекалу.

Касательная к эвольвенте, например в точке X, перпендикулярна к касательной X - 10 окружности.

Построение циклоиды (рис. III.52). Траектория точки А, принадлежащей окружности, перекатываемой без скольжения по прямой, называется циклоидой. Для ее построения от исходного положения А на направляющей прямой откладывается отрезок AAi, равный длине данной окружности 2nR. Окружность и отрезок АА делятся на одинаковое число равных частей. Восставляя перпендикуляры из точек делений прямой АА до пересечения с прямой, проходящей через HYp данной окружности параллельно АА, намечают ряд последовательных положений центра перекатываемой окружности Oi, О2, О3, О12. Описывая из этих центров дуги радиусом R, отмечают точки пересечения с ними прямых, проходящих параллельно АА через точки деления окружности 7, 2, 3, 4 и т. д.: на пересечении горизонтальной